A quantidade de superfície que uma figura plana cobre é chamada de sua área. Sua unidade é centímetros quadrados ou metros quadrados and many others.
Podemos encontrar a área da superfície fechada, encontrando o número de quadrados completos da unidade dentro da figura desenhada em uma folha quadrada. A unidade de área é o centímetro quadrado.
Um retângulo, um quadrado, um triângulo e um círculo são exemplos de figuras planas fechadas.
Nas figuras a seguir, a região sombreada de cada um dos objeto é a superfície ocupada por ele. Nós chamamos de área.
Inside e exterior de uma região:
A parte do plano cercada por uma figura fechada é chamada de região inside e a parte do plano fora da figura fechada é chamada de região externa.
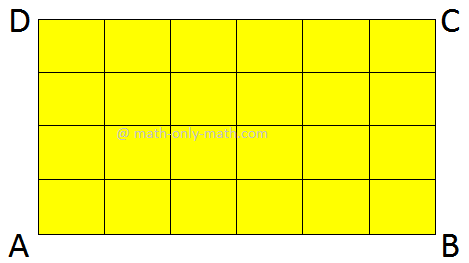
Na figura adjacente, um retângulo ABCD é mostrado. Suas regiões internas e externas também são mostradas aqui.
Área é sempre medido em quadrados e o unidade de unidades quadradas de área (sq. cm., sq. m. ou cm2m2).
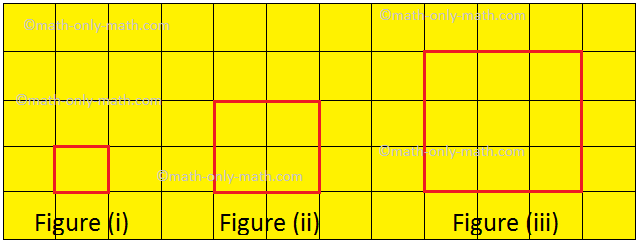
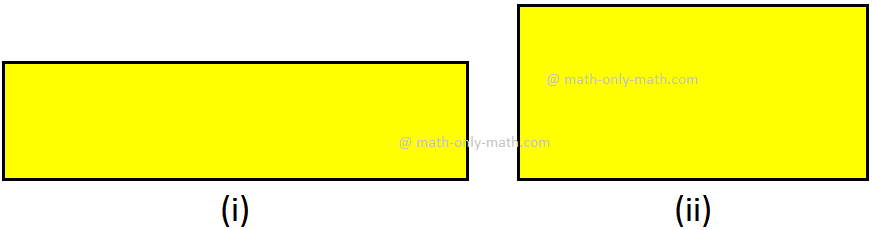
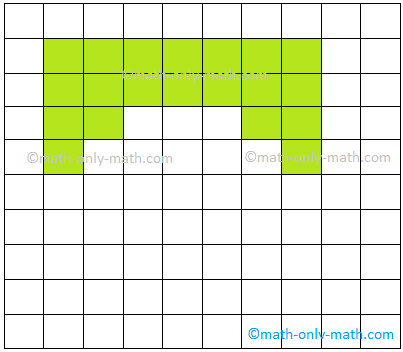
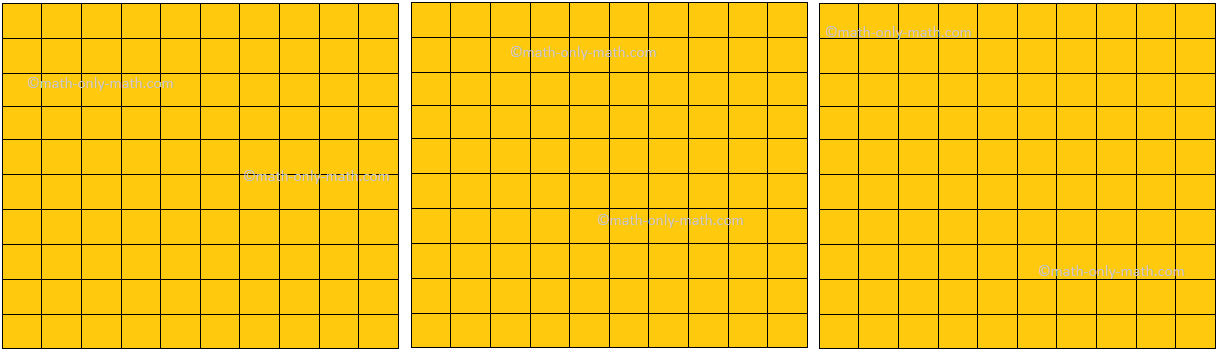
Vamos desenhar alguma forma de plano em uma folha quadrada, como mostrado abaixo.
Aqui, podemos ver que a forma na figura (i) é a menor em tamanho ou podemos dizer que ela inclui menos espaço ou superfície que a Figura (ii) e a Figura (iii). Vamos comparar a superfície do papel fechada por cada formas. A forma na Figura (i) inclui apenas um quadrado de unidade na folha de gráficos. A forma na Figura (ii) inclui 4 quadrados de unidade e a forma na Figura (iii) encerra 9 quadrados de unidade na folha de gráficos. Observamos que formas maiores envolvem mais superfície do que as menores formas. A superfície cercada por uma forma de plano é chamada área.
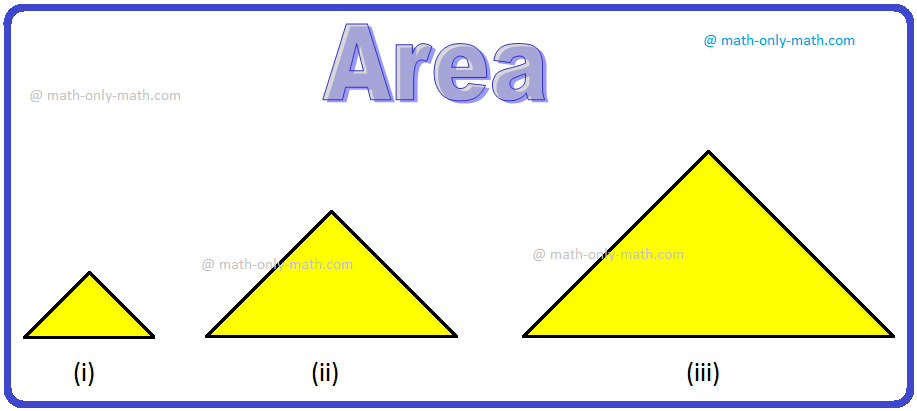
Observe as seguintes figuras:
Qual triângulo é o maior e qual triângulo é o menor em tamanho?
Claramente, o primeiro em triângulo é o menor e o terceiro triângulo é o maior em tamanho.
Como sabemos que o triângulo é o menor e o terceiro triângulo é o maior?
De fato, acabamos de comparar a superfície do papel cercado por cada figura.
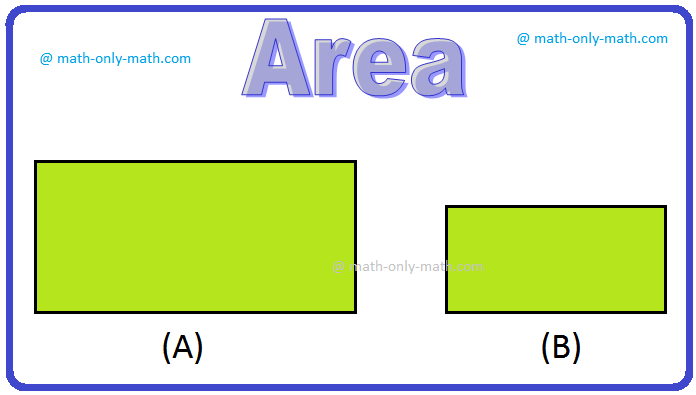
Novamente observe os números:
Qual retângulo é o tamanho maior?
Claramente, o primeiro retângulo é maior em tamanho, porque inclui mais superfície que o outro.
Novamente, observe os números:
Aqui também, a superfície sombreada do primeiro quadrado é menor que a região sombreada do segundo. Portanto, a primeira figura é menor em tamanho.
A partir desses exemplos, fica claro que, quando falamos sobre o tamanho de uma figura plana, consideramos a superfície cercada por ela.
A medida da superfície cercada por uma figura plana é chamada área.
Regiões de medição:
Sabemos que uma superfície plana é chamada de avião. Um quadrado, um triângulo e um círculo são alguns exemplos de formas planas. A quantidade de superfície fechada é chamada de sua área. Podemos calcular a área de uma forma plana desenhada em uma folha quadrada contando os quadrados da unidade fechados por ela.
Para formas irregulares, contamos 2 meios quadrados como um e ignoramos os quadrados cujas menos de meia parte são cercadas pela figura.
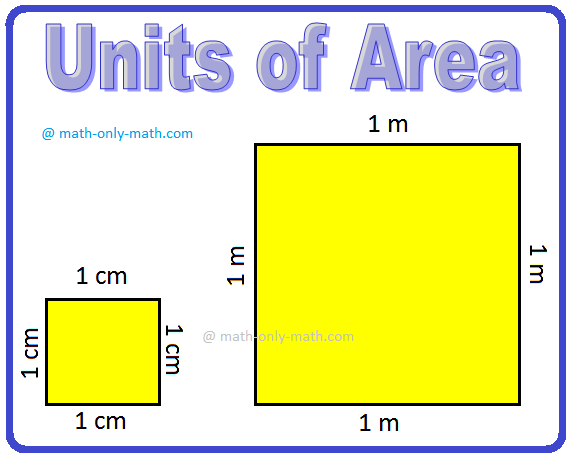
Unidade de área:
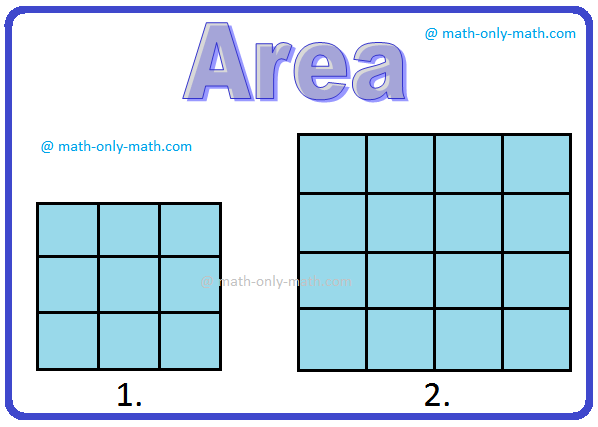
Observe os números:
Você pode dizer qual figura tem a área maior? Aqui é difícil dizer qual figura tem a maior área menor por mera observação. Para decidir qual figura tem a área maior, understand a seguinte atividade.
Cubra as duas figuras com os pedaços de borrachas.
Podemos ver que 8 peças das borrachas cobrem completamente a primeira figura e 9 peças das borrachas cobrem completamente a segunda figura. Dizemos que a área da primeira figura é igual à área de 8 borrachas e a área da segunda figura é igual à área de 9 borrachas. Assim, a segunda figura tem a área maior.
Aqui a face superior (ou inferior) da borracha tem foi tomado como unidade para medir a área de cada figura.
Na atividade acima, se usarmos borrachas maiores, teremos a mesma resposta?
Não, neste caso, a resposta será diferente. Portanto, para obter a mesma resposta sempre, precisamos de uma unidade padrão para medir a área.
Para medir o peso (massa), usamos g ou kg como as unidades padrão.
Para medir a capacidade, usamos Mℓ ou ℓ como unidades padrão.
Para medir o comprimento, usamos MM, CM ou M como unidades padrão.
Da mesma forma, para medir a área de um mm quadrado, cm ou m é considerado a unidade padrão.
A área de um quadrado de 1 mm é expresso como 1 mm quadrado ou mm mm.
A área de um quadrado de lateral 1 cm é expresso como 1 cm quadrado ou 1 cm quadrado.
A área de um quadrado de lado 1 m é expresso como 1 quadrado m ou 1 m².
As áreas maiores são medidas em quilômetros quadrados (km quadrados).
1 km2 é a área do quadrado cujo lado é de 1 km.
A área é medida em unidades quadradas. Um quadrado de 1 cm ou 1 m é usado como unidades padrão. A unidade menor de área é quadrada cm ou sq. Cm. As áreas maiores são medidas em metros e quilômetros.
Medimos uma determinada região por uma região unitária e descobrimos quantas regiões unidades estão contidas na região especificada.
A medida de uma região é chamada de sua área.
A área é sempre expressa em unidades quadradas. As unidades padrão que geralmente são usadas para medir a área são centímetro quadrado e metro quadrado.
A área de um quadrado com lateral 1 cm cada é 1 cm × 1 cm = 1 centímetro quadrado. Em suma, é expresso como CM2 ou sq. cm.
A área de um quadrado com o lado 1 m cada é 1 m × 1 m = 1 metro quadrado. Em suma, é expresso como M2 ou sq. m.
A área é uma medida de qualquer superfície da área, por exemplo, a superfície de uma mesa, a superfície da sua caixa de lápis and many others.
Área é bidimensional.
Significa, para encontrar a área de qualquer superfície necessária para conhecer dois lados.
Observação:
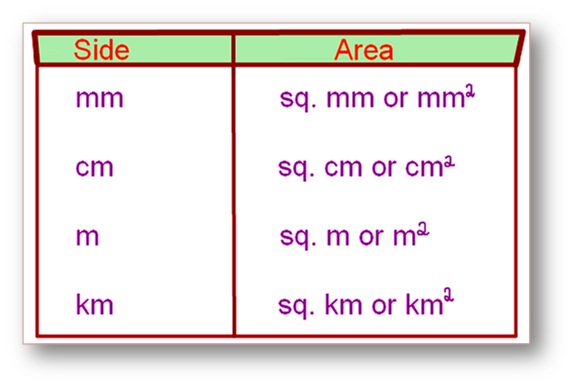
Aqui, discutiremos apenas áreas de quadrado e retângulos. A seguir, é dada uma tabela de unidades de lados e unidades correspondentes para áreas.
Tabela de conversão:
1 m. = 100 cm.
1 m² m. = 10000 sq. Cm.
1 cm. = 10 mm.
1 sq. Cm. = 100 mm mm.
1 km = 1000 m
Para encontrar a área de uma determinada figura, verifique se os lados (comprimento ou largura) estão na mesma unidade de comprimento. Se eles forem fornecidos em unidades diferentes, altere -as para a mesma unidade.
A medida do espaço em uma região é chamada de sua área.
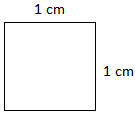
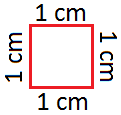
A área de um quadrado de lateral 1 cm é de 1 centímetro quadrado (sq.cm) ou 1 centímetro2 (cm2).
Observe os seguintes quadrados.
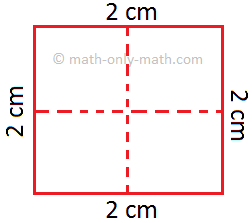
(eu) Na figura abaixo, a linha pontilhada divide o quadrado de 2 cm em 4 quadrados de área igual.
Lado de cada pequeno quadrado = 1 cm
Área de cada pequeno quadrado = 1 cm2
Área whole do quadrado = 4 × 1 cm2 = 4 cm2
Mas sabemos que 2 cm × 2 cm = 4 cm2
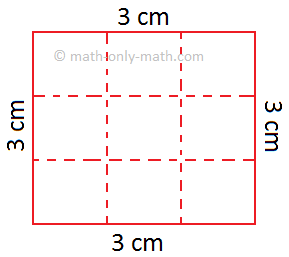
(ii) Na figura determinada, a linha pontilhada divide o quadrado de 3 cm em 9 quadrados de área igual.
Lado de cada pequeno quadrado = 1 cm
Área de cada pequeno quadrado = 1 cm2
Área whole do quadrado = 9 × 1 cm2 = 9 cm2
Mas sabemos que 3 cm × 3 cm = 9 cm2
Área de um quadrado = lado × lado
Por exemplo:
1. Encontre a área de um quadrado de 8 cm.
Lado = 8 cm
Área do quadrado = lado × lado
= 8 cm × 8 cm
= 64 cm2 ou 64 sq.cm
● Dada abaixo, há um retângulo de comprimento 7 cm e largura 3 cm. É dividido em quadrados da área 1 cm2.
Conte o número de quadrados. Existem 21 quadrados.
A área whole do retângulo = área de 21 quadrados
= 21 cm2
Mas sabemos que 7 cm × 3 cm = 21 cm2
Área de um retângulo = comprimento × largura
Por exemplo:
1. Encontre a área de um retângulo cujo comprimento e largura são 9 cm e 3 cm, respectivamente.
Comprimento = 9 cm
Largura = 3 cm
Área do retângulo = comprimento × largura
= 9 cm × 3 cm = 27 cm2
Exemplos resolvidos em regiões de medição:
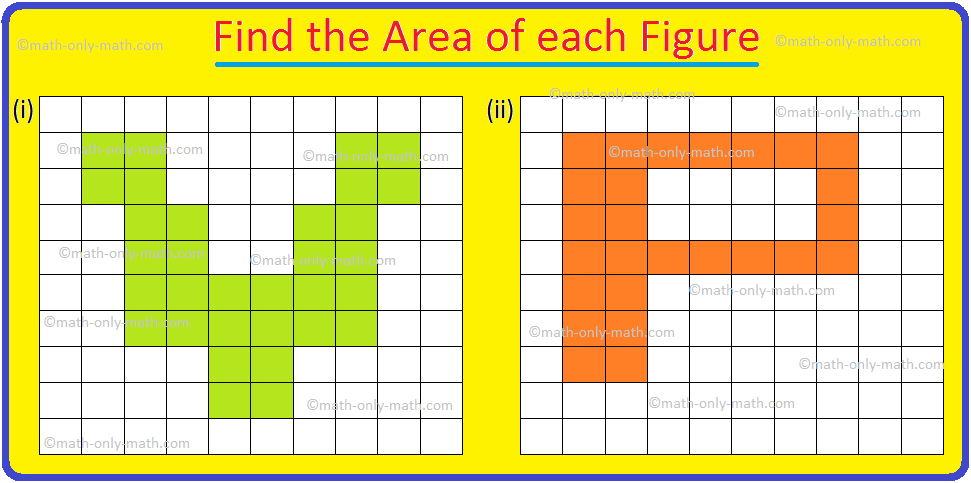
1. Encontre a área das figuras fornecidas em uma folha de gráficos de quadrados de 1 cm × 1 cm.
Solução:
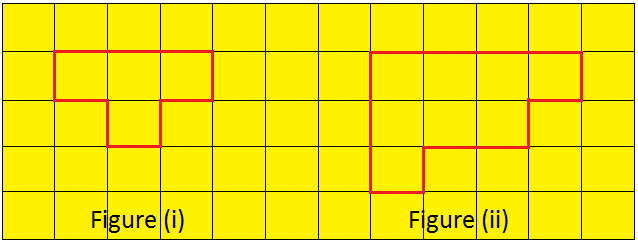
Figura (i):
( frac {1} {2} ) quadrados = 6; Quadrados completos = 6
Área = ( frac {1} {2} ) × 6 + 6 = 9 sq. Cm.
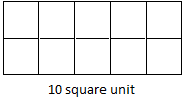
Figura (ii):
Número de quadrados = 12
Área = 12 cm2.
2. Encontre a área das figuras a seguir na folha de gráficos de 1 cm quadrado.
|
Existem 4 quadrados na figura (i). Portanto, a área da figura (i) é de 4 pés quadrados |
Existem 8 quadrados na Figura (ii). Portanto, a área da Figura (II) é de 8 cm quadrados |
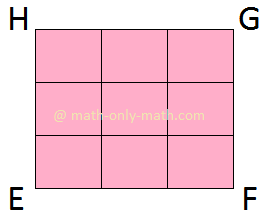
3. Na figura a seguir, a área de cada quadrado menor é de 1 cm quadrado.
Quantos quadrados existem no whole?
|
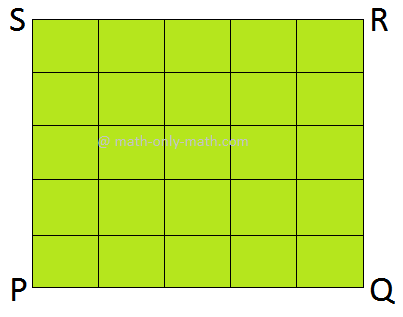
(ii) Aqui, a área de cada quadrado menor é de 1 mm quadrado. Existem 25 tais quadrados. Portanto, a área do Sq. PQRS é de 25 mm mm. |
|
(iii) Aqui, a área de cada quadrado menor é de 1 cm2. Existem 9 tais quadrados. Portanto, os são do EFGH quadrado é de 9 cm quadrados. |
Agora, responda às seguintes perguntas para ter uma rápida revisão do que aprendemos até agora.
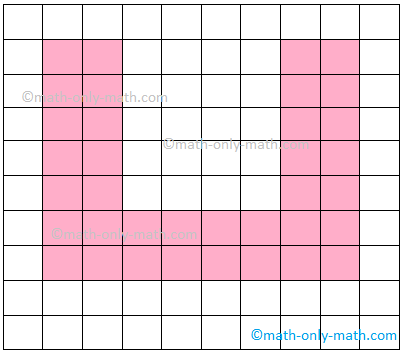
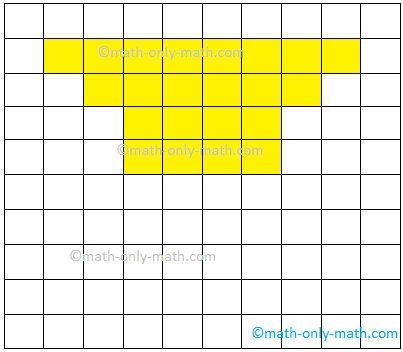
1. Para as figuras dadas, encontre a área de cada figura se cada lado de um quadrado for 1 unidade.
Responder:
(i) Unidades de 32 m²
(ii) 26 unidades quadradas
2. Se a área de cada quadrado for 1 cm quadrado, encontre a área das figuras fornecidas.
(eu) Área =
(ii) Área =
(iii) Área =
(4) Área =
Responder:
(i) 40 pés quadrados
(ii) 36 pés quadrados
(iii) 22 sq. CM
(iv) 20 pés quadrados
3. Desenhe três polígonos do maior tamanho possível nas grades fornecidas e calcule sua área se cada lado de um quadrado for 1 cm.
4. Desenhe qualquer forma nas grades com a seguinte área se cada lado de um quadrado for 1 unidade.
(eu) Área = 9 unidades quadradas
(ii) Área = 20 unidades quadradas
(iii) Área = 15 unidades quadradas
5. Preencha os espaços em branco:
(i) ………………… .. mede a superfície coberta por uma forma 2D.
(ii) A área de um retângulo com comprimento 5 me largura 10 m será …………………… ..
Responder:
(i) Área
(ii) unidades de 50 m²
6. Encontre a área dos seguintes quadrados com lados.
(i) 10 cm
(ii) 9 cm
(iii) 3 cm
(iv) 7 cm
(v) 6 cm
Responder:
6. (i) 100 cm2
(ii) 81 cm2
(iii) 9 cm2
(iv) 49 cm2
(v) 36 cm2
7. Encontre a área de cada um dos seguintes retângulos com:
(i) Comprimento = 6 cm de largura = 4 cm
(ii) comprimento = 5 cm de largura = 2 cm
(iii) comprimento = 10 cm de largura = 6 cm
(iv) Comprimento = 7 cm de largura = 4 cm
Responder:
7. (i) 24 cm2
(ii) 10 cm2
(iii) 60 cm2
(iv) 28 cm2
● Área.
Encontrar a área de um retângulo quando o comprimento e a largura são de diferentes unidades.
Para encontrar comprimento ou largura quando a área de um retângulo é dada.
Para encontrar o custo de pintura ou lavoura quando a área e o custo por unidade são fornecidos.
Para encontrar o número de tijolos ou ladrilhos quando a área de caminho e tijolo é fornecida.
Planilha na área de um quadrado e retângulo
Problemas de matemática da 5ª série
De que área é em matemática? para a página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.