Ao converter decimais em frações, sabemos que um decimal sempre pode ser convertido em uma fração usando as seguintes etapas:
Passo I: Obter o decimal.
Etapa II: Remova os pontos decimais do decimal dado e tome como numerador.
Etapa III: Ao mesmo tempo, escreva no denominador, tanto zero ou zeros à direita de 1 (um) (por exemplo, 10, 100 ou 1000 and so on.), pois há número de dígitos ou dígitos na parte decimal. E depois simplifique.
Podemos expressar um número decimal como uma fração mantendo o número fornecido como numerador sem um ponto decimal e escrevendo 1 no denominador, seguido de tantos zeros à direita quanto o número de locais decimais no número decimal dado.
Por exemplo:
(i) 124.6 = ( frac {1246} {10} )
(ii) 12.46 = ( frac {1246} {100} )
(iii) 1.246 = ( frac {1246} {1000} )
O problema nos ajudará a entender como converter decimal em fração.
Em 0,7 Mudaremos o decimal para a fração.
Primeiro, escreveremos o decimal sem o ponto decimal como numerador.
Agora, no denominador, escreva 1 seguido por um zeros, pois há 1 dígito na parte decimal do número decimal.
= ( frac {7} {10} )
Portanto, observamos que 0,7 (decimal) é convertido em ( frac {7} {10} ) (fração).
Regras de trabalho para conversão de um decimal em uma fração:
Para converter um decimal em fração, seguimos as seguintes etapas
Regras de trabalho
Passo I: Escreva o número fornecido sem ponto decimal como numerador da fração.
Etapa II: Escreva 1 no denominador seguido por tantos zeros quanto o número de locais decimais no número fornecido.
Etapa III: Reduza a fração nos termos mais baixos e, se necessário, mude para um número misto.
Exemplos resolvidos na conversão de decimais em frações
1. Converta 6,75 em uma fração.
Solução:
Numerador da fração = 675
Denominador de fração = 100 (porque os lugares decimais são 2, portanto, coloque 2 zeros após 1.)
Então, 6.75 = ( frac {625} {100} )
= ( frac {625 ÷ 25} {100 ÷ 25} )
= ( frac {27} {4} )
= 6 ( frac {3} {4} )
2. Converta 924.275 em uma fração.
Solução:
Numerador da fração = 924275
Denominação da fração = 1000 (porque os lugares decimais são 3, portanto, colocam 3 zeros após 1.)
Agora, 924.275 = ( frac {924275} {1000} )
= ( frac {924275 ÷ 25} {1000 ÷ 25} )
= ( frac {36971} {40} )
= 924 ( frac {11} {40} )
Exemplos de trabalho sobre a conversão de decimais em frações:
1. Converter cada um dos seguintes em frações.
(i) 3,91
Solução:
3.91
Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por dois zeros, pois existem 2 dígitos na parte decimal do número decimal.
= ( frac {391} {100} )
(ii) 2.017
Solução:
2.017
= ( frac {2.017} {1} )
= ( frac {2.017 × 1000} {1 × 1000} ) ⟹
No denominador, escreva 1 seguido por três zeros, pois existem 3 dígitos na parte decimal do número decimal.
= ( frac {2017} {1000} )
2. Converta 0,0035 em fração na forma mais simples.
Solução:
0,0035
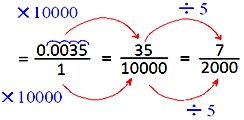
Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por quatro zeros à direita de 1 (um), pois existem 4 locais decimais no número decimal fornecido.
Agora, reduziremos a fração ( frac {35} {10000} ) e obtida no seu termo mais baixo ou na forma mais simples.
= ( frac {7} {2000} )
3. Expresse os seguintes decimais como frações da forma mais baixa:
(i) 0,05
Solução:
0,05
= ( frac {5} {100} ) ⟹ Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por dois zeros à direita de 1 (um), pois existem 2 locais decimais no número decimal fornecido.
= ( frac {5 ÷ 5} {100 ÷ 5} ) ⟹
Reduza a fração obtida ao seu termo mais baixo.
= ( frac {1} {20} )
(ii) 3,75
Solução:
3.75
= ( frac {375} {100} ) ⟹ Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por dois zeros à direita de 1 (um), pois existem 2 locais decimais no número decimal fornecido.
= ( frac {375 ÷ 25} {100 ÷ 25} ) ⟹ Reduza a fração obtida à sua forma mais simples.
= ( frac {15} {4} )
(iii) 0,004
Solução:
0,004
= ( frac {4} {1000} ) ⟹ Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por três zeros à direita de 1 (um), pois existem 3 locais decimais no número decimal fornecido.
= ( frac {4 ÷ 4} {1000 ÷ 4} ) ⟹ Reduza a fração obtida ao seu termo mais baixo.
= ( frac {1} {250} )
(iv) 5.066
Solução:
5.066
= ( frac {5066} {1000} ) ⟹ Escreva o número decimal fornecido sem o ponto decimal como numerador.
No denominador, escreva 1 seguido por três zeros à direita de 1 (um), pois existem 3 locais decimais no número decimal fornecido.
= ( frac {5066 ÷ 2} {1000 ÷ 2} ) ⟹ Reduza a fração obtida à sua forma mais simples.
= ( frac {2533} {500} )
Mais exemplos sobre a conversão de decimais em frações:
Vamos considerar mais alguns exemplos para converter decimais em frações
PASSOS
Passo I: Remova o ponto decimal e escreva o número como o numerador da fração necessária
Etapa II: Escreva 1 como denominador.
Etapa III: Conte o número de dígitos à direita do ponto decimal no decimal e escreva o mesmo número de zero à direita de 1 no denominador
4. Converta 2.7 em uma fração
Solução:
27 = ( frac {27} {10} )
= 2 ( frac {7} {10} )
Portanto, 27 = 2 ( frac {7} {10} )
5. Converta 32.47 em uma fração.
Solução:
32.47
O denominador terá dois zeros à direita de 1 porque o decimal tem dois dígitos à direita do ponto decimal,
32.47 = ( frac {3247} {100} )
= 32 ( frac {47} {100} )
Portanto, 32.47 = 32 ( frac {47} {100} )
6. Converta 2.255 em uma fração
Solução:
2.255 = ( frac {2255} {1000} );
= 2255/1000
(Sempre reduzimos a fração para seus termos mais baixos.)
= ( frac {451} {200} )
= 2 ( frac {51} {200} )
Assim, 2.255 = 2 ( frac {51} {200} )
7. Converta os seguintes decimais em uma fração
(i) 425.25
(ii) 318.4
Solução:
(i) 425.25 = ( frac {42524} {100} )
= 42525/100
(Sempre reduzimos a fração aos seus termos mais baixos.)
= ( frac {1701} {4} )
= 425 ( frac {1} {4} )
Assim, 425.25 = 425 ( frac {1} {4} )
(ii) 318.4 = ( frac {3184} {10} )
= 3184/10
(Sempre reduzimos a fração aos seus termos mais baixos.)
= ( frac {1592} {5} )
= 318 ( frac {2} {5} )
Assim, 318.4 = 318 ( frac {2} {5} )
Planilha sobre a conversão de decimais em frações:
1. Converta os números decimais fornecidos em frações no termo mais baixo:
(i) 1.3
(ii) 0,004
(iii) 4.005
(iv) 7.289
(v) 0,56
(vi) 21.08
(vii) 0,067
(viii) 6.66
Respostas:
1. (i) ( frac {13} {10} )
(ii) ( frac {1} {250} )
(iii) ( frac {801} {200} )
(iv) ( frac {7289} {1000} )
(v) ( frac {14} {25} )
(vi) ( frac {527} {25} )
(vii) ( frac {67} {1000} )
(viii) ( frac {333} {50} )
2. Converta as seguintes decimais em frações comuns nos termos mais baixos:
(i) 0,7
(ii) 0,15
(iii) 0,085
(iv) 27.35
(v) 0,27
(vi) 2.08
(vii) 17.2
(viii) 5.005
(ix) 206.007
(x) 0,003
(xi) 71.035
(xii) 35.607
Responder:
2. (i) ( frac {7} {10} )
(ii) ( frac {3} {20} )
(iii) ( frac {17} {200} )
(iv) 27 ( frac {7} {20} )
(v) ( frac {27} {100} )
(vi) 2 ( frac {2} {5} )
(vii) 17 ( frac {1} {5} )
(viii) 5 ( frac {1} {200} )
(ix) 206 ( frac {7} {1000} )
(x) ( frac {3} {1000} )
(xi) 71 ( frac {7} {200} )
(xii) 35 ( frac {607} {1000} )
● Conceito relacionado
● Decimais
● Como e diferente de decimais
● Conversão de decimais diferentes para decimais
● Expansão decimal e fracionária
● Convertendo decimais em frações
● Conversão de frações em decimais
● Repete ou recorrente decimal
● Regras de Bodmas/Pemdas – envolvendo decimais
● Regras de Pemdas – envolvendo números inteiros
● Regras de Pemdas – envolvendo decimais
● Regras de Bodmas – envolvendo números inteiros
● Conversão de decimal recorrente puro em fração vulgar
● Conversão de decimais recorrentes mistos em frações vulgares
● Decimais arredondados para o número inteiro mais próximo
● Decimais arredondados para os décimos mais próximos
● Decimais arredondados para os centésimos mais próximos
● Simplifique decimais envolvendo decimais de adição e subtração
● Multiplicando decimal por um número decimal
● Multiplicando decimal por um número inteiro
● Dividindo decimal por um número inteiro
● Dividindo decimal por um número decimal
Problemas de matemática da 7ª série
Da conversão de decimais em frações para a página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.








