4 de fevereiro de 2025
4 Min Learn
Os matemáticos resolvem o infame ‘sofá em movimento’ Downside ‘
Qual é o maior sofá que pode virar uma esquina? Depois de 58 anos, finalmente sabemos
Para aqueles que lutaram um sofá volumoso ao redor de um canto apertado e lamentou: “Isso vai se encaixar?” Os matemáticos ouviram seus pedidos. O “Problema do sofá em movimento” da Geometry pede a maior forma que pode girar um ângulo reto em um corredor estreito sem ficar preso. O problema ficou sem solução por quase 60 anos até novembro, quando Jineon Baek, um pós -doutorado na Universidade Yonsei em Seul, postou um papel on-line alegando resolvê -lo. A prova de Baek ainda não passou por uma revisão completa dos pares, mas os passes iniciais de matemáticos que conhecem Baek e o problema do sofá em movimento parecem otimistas. Somente o tempo dirá por que levou Baek 119 páginas para escrever o que Ross Geller da Sitcom Amigos disse em uma palavra.
É improvável que a solução ajude você a mudar o dia, mas à medida que a matemática da fronteira cresce mais abstrato, os matemáticos têm um gosto especial por problemas não resolvidos que qualquer um pode entender. De fato, o standard fórum de matemática MathOverflow mantém uma lista de “Não é especialmente famoso e aberto problemas que qualquer um pode entender”E o problema do sofá em movimento atualmente ocupa o segundo lugar na lista. Ainda assim, toda prova expande nosso entendimento, e as técnicas usadas para resolver o problema do sofá em movimento provavelmente se prestarão a outros quebra -cabeças geométricos no caminho.
As regras do problema, que o matemático canadense Leo Moser primeiro formalmente posado Em 1966, envolva uma forma rígida – para que as almofadas não cedam quando pressionadas – girando um ângulo reto em um corredor. O sofá pode ter qualquer forma geométrica; Não precisa se parecer com um sofá actual. Tanto a forma quanto o corredor são bidimensionais. Think about que o sofá pesa muito para levantar, e você só pode deslizá -lo.
Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
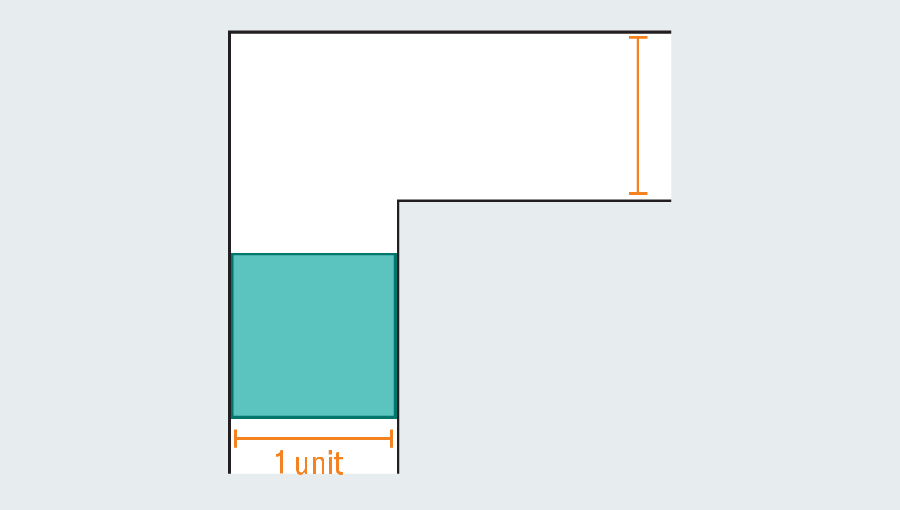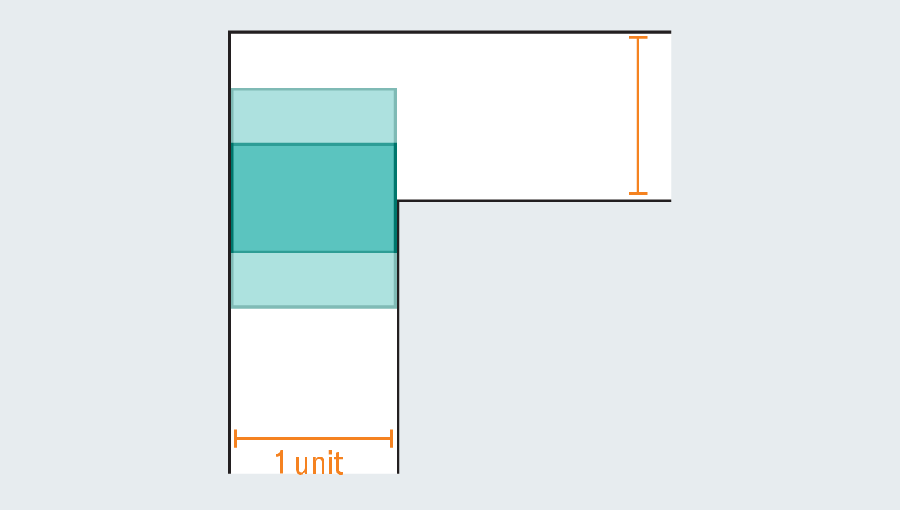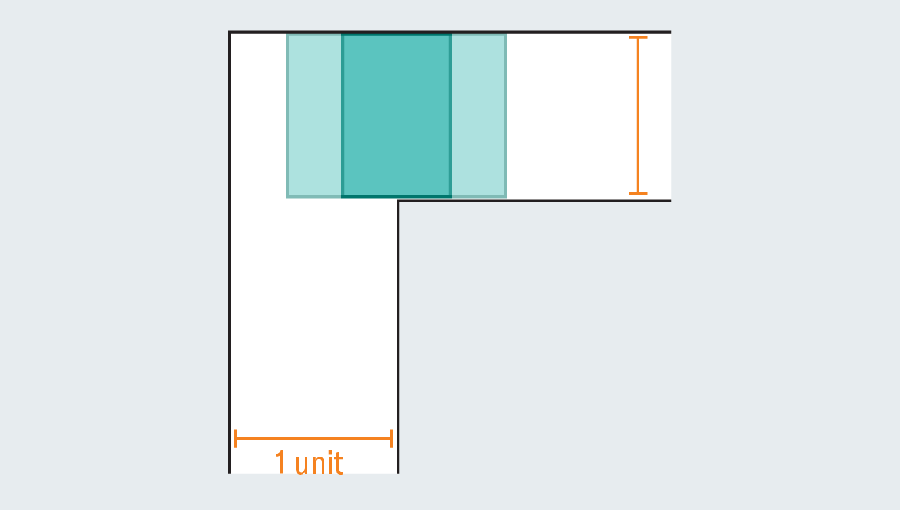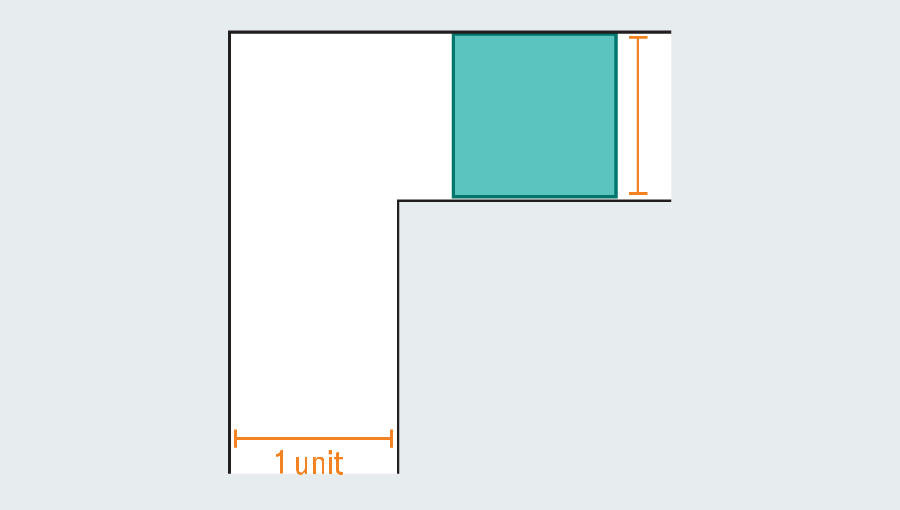
Um rápido passeio pela história do problema revela o extenso esforço que os matemáticos investiram nela – eles não eram batatas. Diante de um corredor vazio, qual é a maior forma que você pode espremer através dele? Se cada perna do corredor mede uma unidade (a unidade específica não importa), podemos facilmente escorregar um quadrado um a um através da passagem. Alongando o quadrado para formar um retângulo falha instantaneamente, porque uma vez que atinge a torção no corredor, não tem espaço para girar.
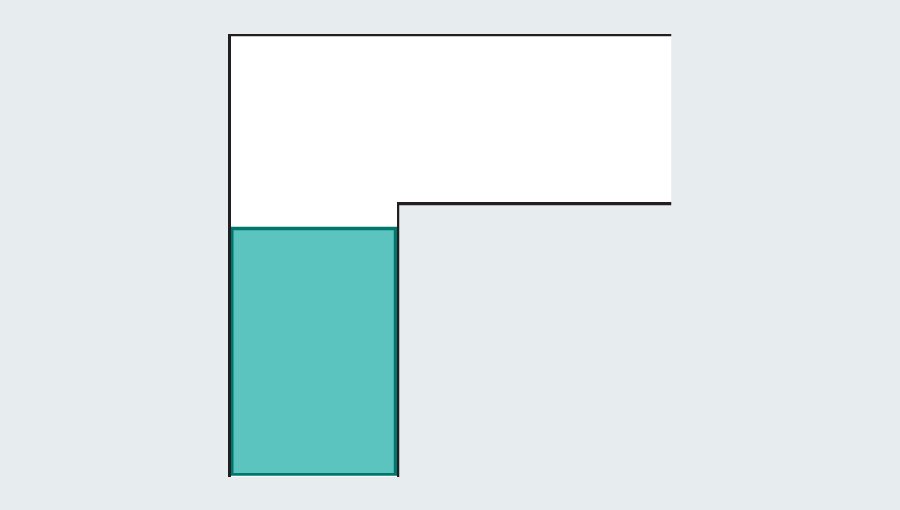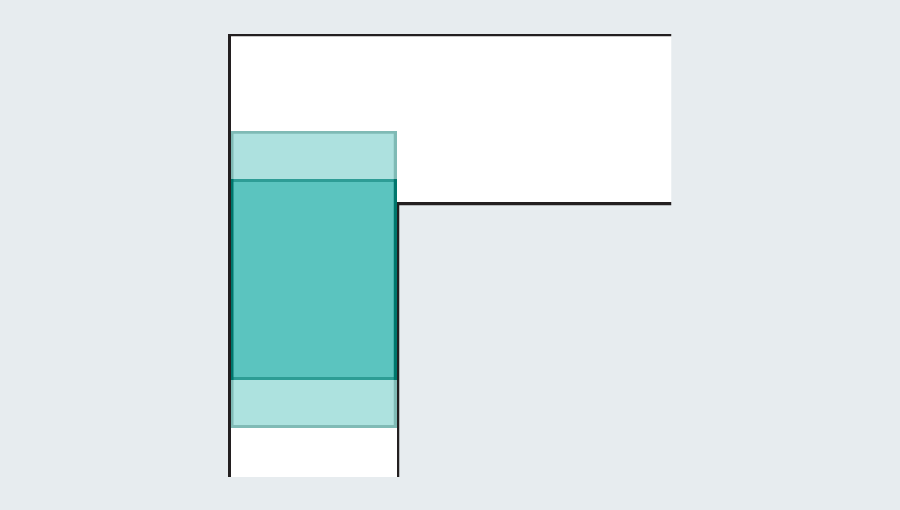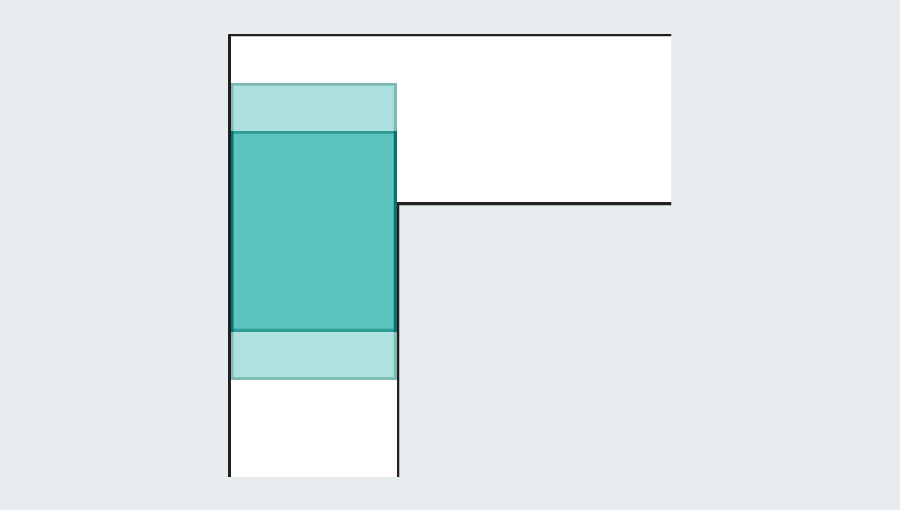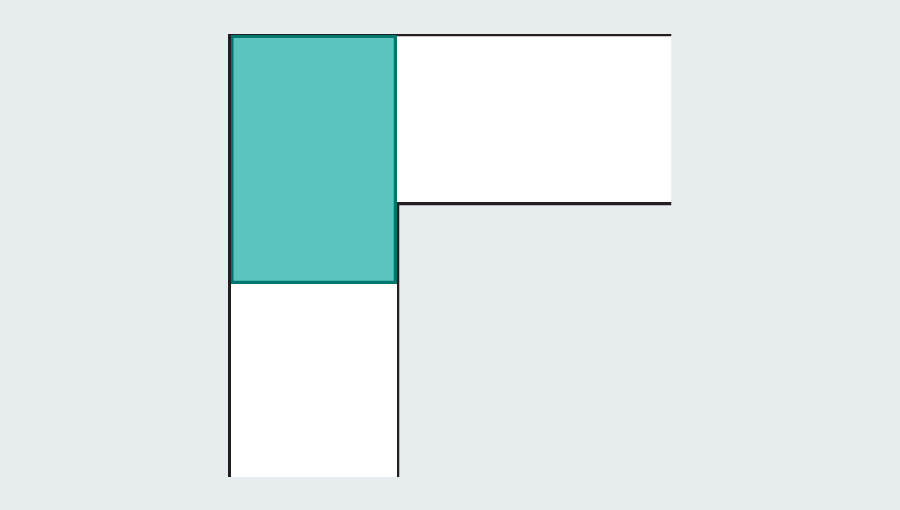
No entanto, os matemáticos perceberam que podem se tornar maiores, introduzindo formas curvas. Considere um semicírculo com um diâmetro (a base reta) de 2. Quando atinge a curva, grande parte ainda se abriga na primeira mão do corredor, mas a borda arredondada deixa espaço suficiente para limpar o canto.
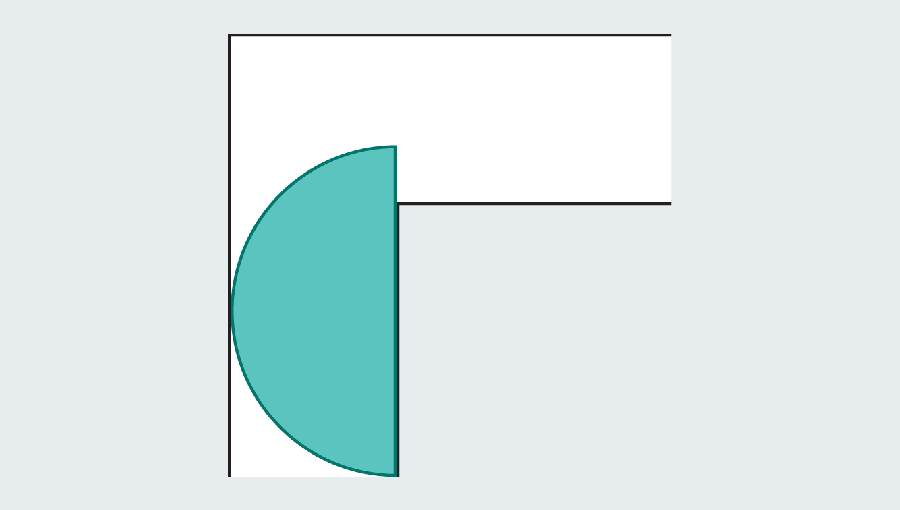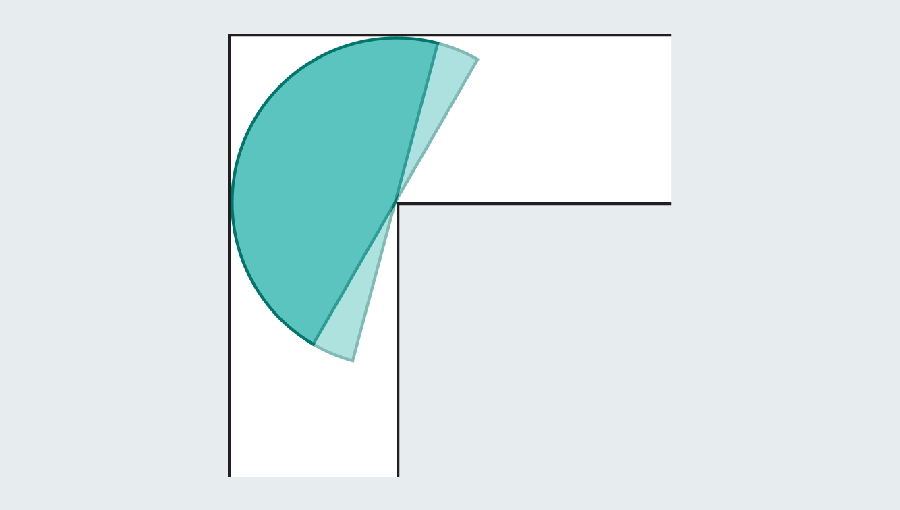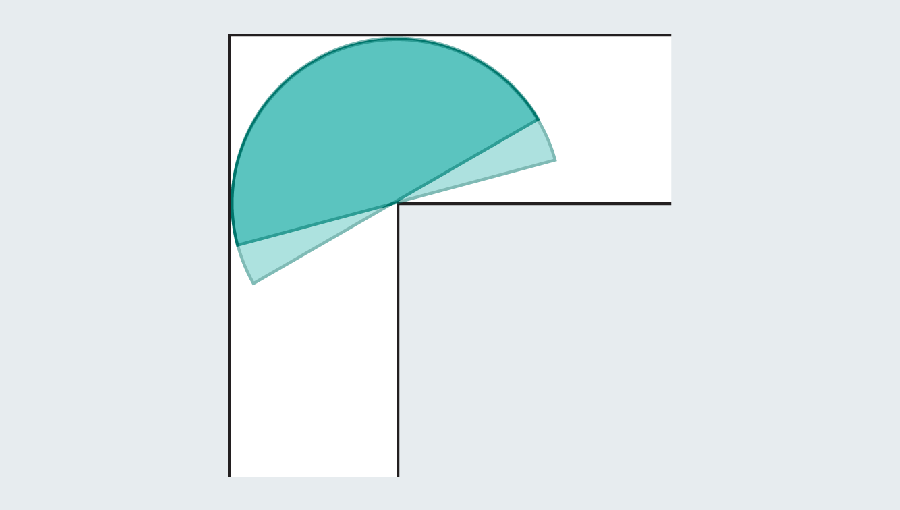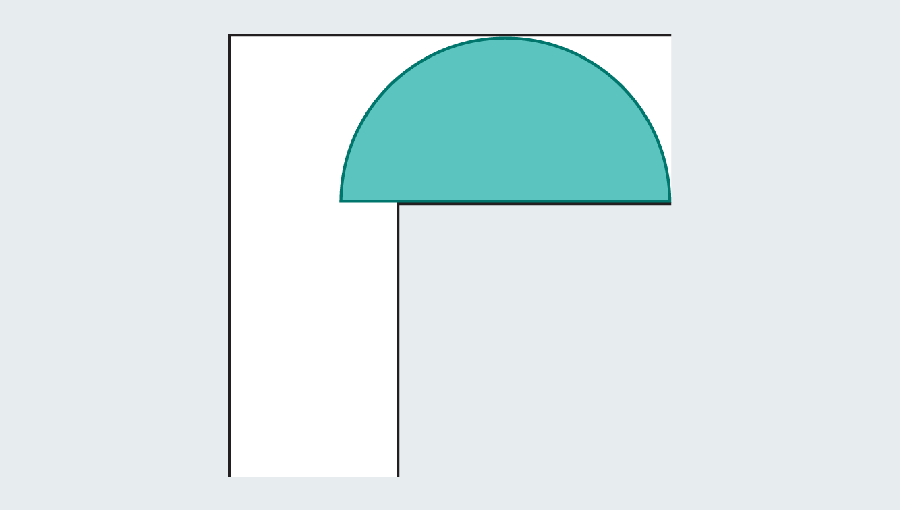
Lembre -se de que o objetivo é encontrar o maior “sofá” que desliza na esquina. Descobrir nossas fórmulas de geometria do ensino médio, podemos calcular a área do semicírculo como π/2, ou aproximadamente 1,571. O semicírculo dá uma melhoria significativa sobre o quadrado, que tinha uma área de apenas 1. Infelizmente, ambos pareceriam estranhos em uma sala de estar.
Resolver o problema do sofá em movimento exige que você não apenas otimize o tamanho de uma forma, mas também o caminho Essa forma atravessa. A configuração permite dois tipos de movimento: deslizando e girando. O sofá quadrado deslizou apenas, enquanto o semicírculo deslizou, depois girou ao redor da curva e depois deslizou novamente do outro lado. Mas os objetos podem deslizar e girar ao mesmo tempo. Matemático Dan Romik, da Universidade da Califórnia, Davis, tem observado que uma solução para o problema deve otimizar os dois tipos de movimento simultaneamente.
Matemático britânico John Hammersley descobriu em 1968 que esticando o semicírculo pode Compre um sofá maior para você, se você esculpir um pedaço para lidar com aquele canto irritante. Além disso, o sofá de Hammersley tira proveito de um movimento deslizante híbrido mais movimento rotativo. O sofá resultante parece um telefone fixo:

Amanda Montañez; Fonte: “Ao mover um sofá ao redor de uma esquina”, de Joseph L. Gerver, em Geometriae dedicata, Vol. 42, nº 3; Junho de 1992 (referência)
A otimizar as diferentes variáveis produz um sofá com área π/2 + 2/π, ou aproximadamente 2,2074. Esta é uma enorme atualização do semicírculo, semelhante a se mudar de um assento de amor para uma seção. Mas o progresso parou lá por 24 anos. A próxima melhoria significativa seria a última. Em 1992 Joseph Gerver revelou Uma obra -prima de carpintaria matemática, que agora sabemos ser o maior sofá possível.
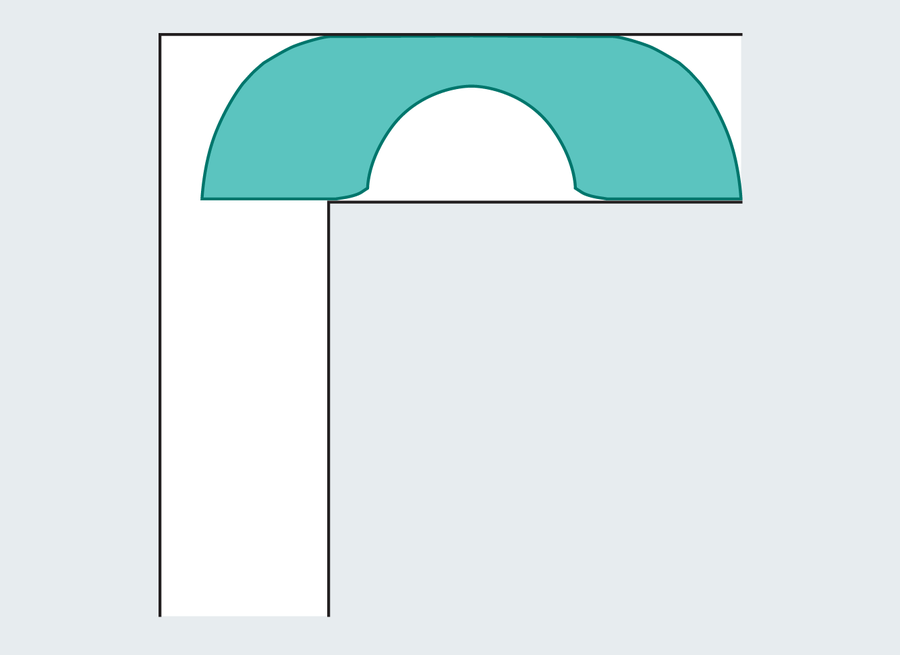
Amanda Montañez; Fonte: “Ao mover um sofá ao redor de uma esquina”, de Joseph L. Gerver, em Geometriae dedicataVol. 42, nº 3; Junho de 1992 (referência)
Você seria perdoado por sentir déjà vu agora. O sofá de Gerver parece idêntico ao de Hammersley, mas é uma construção muito mais complicada. Gerver costurou 18 curvas distintas para formar sua forma. Em uma inspeção mais detalhada, você pode identificar algumas diferenças, especialmente as bordas chanfradas na base do recorte arredondado.
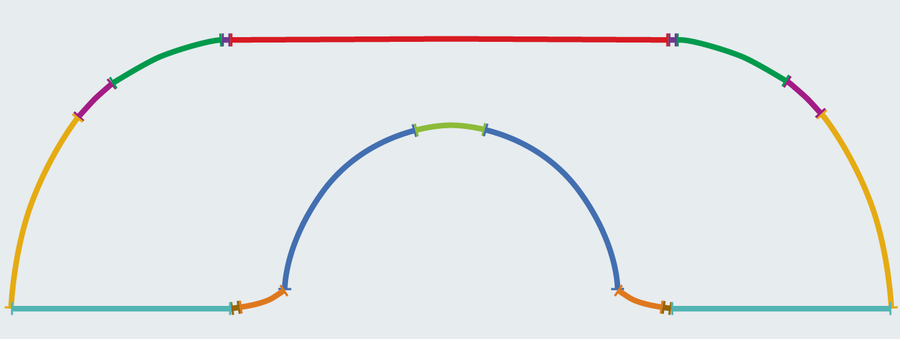
Amanda Montañez; Fonte: “Ao mover um sofá ao redor de uma esquina”, de Joseph L. Gerver, em Geometriae dedicataVol. 42, nº 3; Junho de 1992 (referência)
A área de triunfo de Gerver mede as unidades de 2.2195. Surpreendentemente, o sofá relativamente simples de Hammersley só caiu cerca de 0,012, com menos de ideally suited. Embora apenas um skosh maior que seu antecessor, Gerver suspeitou que sua descoberta atingisse o tamanho máximo possível. Ele não podia provar isso. E nem ninguém mais poderia por mais 32 anos.
Baek terminou seu Ph.D. em 2024 e escreveu sua tese sobre o problema do sofá em movimento, contribuindo com várias idéias incrementais. Nesse mesmo ano, ele costurou todas as suas novas idéias juntas em um impressionante Opus Isso não prova que o sofá maior que o de Gerver pode espremer o corredor. Rachar um problema aberto de longa information é um sonho para qualquer matemático, muito menos um tão cedo em sua carreira. Se o trabalho de Baek suportar o escrutínio, ele provavelmente se encontrará em alta demanda por professores. A menos que ele gire a fabricação de móveis.







