Uma divisão por zero é principalmente uma questão algébrica. O raciocínio, portanto, segue o padrão indireto da maioria das provas algébricas:
E se fosse permitido?
Então teríamos uma contradição, e uma contradição é o maior inimigo do rigor matemático. Muitos estudantes tentaram encontrar uma maneira de dividir por zero uma vez na vida. Para ser sincero: é possível! Poderíamos permitir isso! No entanto, isso teria um preço. Tivemos que renunciar a outras leis que não queríamos perder; acima de tudo, o fato de que ##0## e ##1## são dois números diferentes. Uma divisão por zero muitas vezes resulta na equação ##1=0## o que tornaria ambos bastante inúteis. Mas também causa problemas para outras regras e leis, muitas vezes inesperadas, das quais não queremos abrir mão.
Por que a divisão por zero é uma má ideia, pois implica…
10. 1=0.
Este é o argumento mais curto de todos: $$ dfrac{1}{0}=x Longleftrightarrow 1=xcdot 0=0 $$
9. Todos os números são iguais.
$$acdot 0=bcdot 0 Longrightarrow dfrac{a}{0}=dfrac{b}{0}=ba^{-1}cdotdfrac{a}{0}Longrightarrow ba ^{-1}=1Longrightarrow a=b$$
8. O numerador ou o denominador contam?
Um zero como numerador faz com que um quociente desapareça e, se o numerador e o denominador forem iguais, o quociente se torna um.
$$dfrac{1}{0}=x Longleftrightarrow 1=xcdot 0=xcdot(1-1)stackrel{(D)}{=}xcdot 1-xcdot 1= xx =0$$ o que novamente contradiz ##1neq 0.##
3. O infinito não é uma opção.
A dificuldade ao definir $$dfrac{1}{0}:=infty $$ é que o infinito não é um número. Tal definição apenas desloca a ambigüidade de uma divisão por zero para a ambigüidade de um número infinitamente grande. número. Os problemas são óbvios: $$ start{matriz} infty &+&infty &=&infty &stackrel{?}{Longrightarrow } &infty &= &0 infty &cdot& infty &=&infty &stackrel{?}{Longrightarrow } &infty &= &1 finish{matriz} $$ E continua assim. O infinito não está bem definido. É mais como uma lata grande que engole tudo.
Vamos ver se a regra de L’Hôpital pode nos ajudar, $$ displaystyle{lim_{x to 0}dfrac{f(x)}{g(x)}=lim_{x to 0}dfrac{f'(x)}{g'(x)} } $$ onde zeros e infinitos à esquerda são explicitamente permitidos e apenas ##g'(0)neq 0## e diferenciabilidade à direita são necessários. A condição em ##g'(0)## bloqueia a configuração direta ##g’=0## ou ##g=0.## Se definirmos ##g'(x)=1## tal que o a condição é válida, obtemos ##g(x)=x## e um denominador zero não está à vista. Se considerarmos ##f(x)=x^{-1}## e ##f'(x)=-x^{-2}## acabamos com $$ infty = lim_{x to 0}dfrac{1}{xcdot x}=lim_{x to 0}dfrac{-1}{x^2cdot 1}=-infty $$ o que é obviamente um problema. A diferenciabilidade ausente em ##x=0## causa uma contradição.
2. O ponto de vista geométrico.
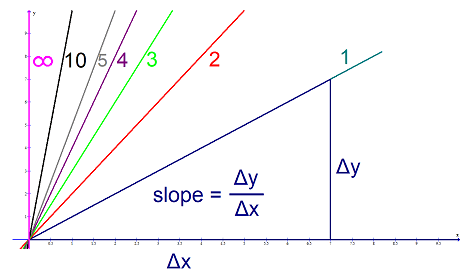
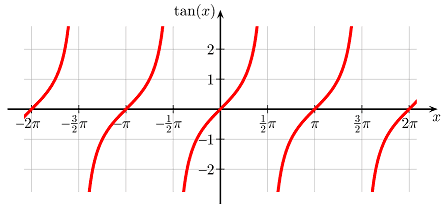
Uma inclinação de ##dfrac{1}{0}## de uma linha reta é uma linha vertical, ou seja, uma linha de inclinação infinita. Já vimos que o infinito não é uma boa escolha. É a singularidade da função tangente em ##pi/2## e nos deparamos com a mesma miséria. Não só temos um poste, mas também temos uma mudança de sinal de ##-infty ## para ##infty ## dependendo se nos aproximamos pela esquerda ou pela direita.
1. ##mathbf{0notinmathbb{F}-{0}.}##
O que parece ser o argumento mais trivial é na verdade o mais sutil e o meu favorito: ##0## como o elemento neutro de adição não faz parte do grupo multiplicativo ##mathbb{F}^*=mathbb{F}-{0}## de um campo ##mathbb{F}.## Não tem nada a ver com multiplicação. A questão de um inverso multiplicativo do elemento neutro da adição simplesmente não ocorre. Surge apenas do nosso desejo de considerar os campos como um conjunto com duas operações. No entanto, eles consistem em dois conjuntos com duas operações: ##(mathbb{F},+)## e ##(mathbb{F}^*,cdot)##. Os conjuntos têm muitos elementos em comum, $$ mathbb{F}^* ;subset; mathbb{F}, $$ mas eles não são iguais.
Então, por que o grupo aditivo contém o elemento neutro da multiplicação, mas o grupo multiplicativo não contém o elemento neutro da adição? Isso se deve principalmente à maneira como construímos campos numéricos: $$ mathbb{N}subset mathbb{Z}subset mathbb{Q}quadtext{ ou }quadmathbb{N}subset mathbb{Z}subset mathbb{Z}_p= matemáticabb{Z}/pmathbb{Z},. $$ Começamos com um grupo aditivo, descobrimos uma estrutura em anel, e caso obtenhamos um domínio integral, nosso anel permite um campo quociente. Agora, zero é um divisor de zero, portanto, fora do conjunto de elementos para os quais podemos construir quocientes; pelo menos não pelo método common $$ dfrac{a}{b} sim dfrac{s}{t} Longleftrightarrow acdot t= bcdot s $$ e contanto que ##1neq 0.## Os anéis não contenham necessariamente o elemento ##1.## Por exemplo, todos os polinômios ##p(x)## com ##p(0)=0## construir um anel sem ##1.## Por outro lado, ##mathbb{Z}/nmathbb{Z}## é apenas um domínio integral, ou seja, permite um campo de quociente, se ##n## for melhor. Estas são as restrições com as quais teremos que lidar se seguirmos o caminho construtivo de um grupo aditivo sobre um anel até um campo. Se começássemos do zero com dois grupos diferentes e procurássemos uma combinação, terminaríamos com produtos livres, diretos ou semidiretos, que são assuntos algébricos diferentes.
Adição e multiplicação em um corpo são conectadas apenas pelas leis distributivas herdadas de sua estrutura em anel $$ acdot (b+c)=acdot b+acdot c quadtext{ e }quad(a+b)cdot c= acdot c+bcdot c $$ Essas duas equações são as únicas onde ambas as operações se encontram. Já vimos que usá-los para definir ##frac{1}{0}## leva a ##1=0.## Isso não pode mais ser um campo, pois ##1## seria um divisor de zero e como tal não poderia fazer parte do grupo multiplicativo, o que é uma contradição.
Reais Estendidos e Hiperreais
O estendido números reais são ##overline{mathbb{R}}=mathbb{R}cup {pm infty}.## Eles desempenham um papel na análise vista do ponto de vista teórico da medida, principalmente para simplificar declarações sobre intervalos ou possíveis limites. Hewitt, Stromberg (Análise Actual e Abstrata, GTM 25) os definem da seguinte forma (negrito meu).
Definição: ##infty ## e ##-infty ## são dois distintos objetos, nenhum dos quais é um número actual. O conjunto ##overline{mathbb{R}}## é conhecido como o conjunto de números reais estendidos. Fazemos ##overline{mathbb{R}}## uma ordem linear definir tomando a ordem common em ##mathbb{R}## e definindo ##-infty
O cuidado especial que Hewitt e Stromberg tomam para evitar que infinitos sejam confundidos com números nos mostra que reais estendidos não resolverão nosso problema de transformar ##frac{1}{0}## em um número. Os números reais estendidos são principalmente uma topológico em vez de um conceito algébrico, e dividindo pontos ou sólitons dificilmente é uma abordagem promissora.
Quando Newton e Leibniz realizaram seu cálculo diferencial com “fluxões” ou “mônadas”, eles usaram números infinitesimais, e Euler e Cauchy também os consideraram úteis. No entanto, estes números foram vistos com ceticismo desde o início. Como a análise foi colocada em uma base rigorosa pela introdução da definição do limite épsilon-delta e da definição de números reais por Cauchy, Weierstrass e outros no século XIX, as quantidades infinitesimais não eram mais necessárias. No entanto, Abraham Robinson mostrou na década de 1960 como números infinitamente grandes e pequenos podem ser definidos de forma estritamente formal, abrindo o campo da análise não padronizada com os chamados números hiperreais. ##;{}^*mathbb{R}.## (de.wikipedia.org: Números hiperreais) 1)
Os números hiperreais, termo introduzido por Edwin Hewitt em 1948, satisfazem o princípio de transferência, uma versão rigorosa da lei heurística da continuidade de Leibniz. É o conceito central que faz com que a análise fora do padrão seja pelo menos uma análise. Isso significa que todas as afirmações verdadeiras na análise actual, ou seja, sobre ##mathbb{R},## permanecem verdadeiras na análise não padrão, ou seja, sobre ##{}^*mathbb{R}.## Um exemplo de como os hiperreais trabalho é a derivada de uma função $$ f'(x)=stleft(dfrac{f(x+varepsilon )-f(x)}{varepsilon }proper) $$ onde ##varepsilon ## é um infinitesimal e ##st## é a função parte padrão que mapeia qualquer número hiperreal para o número actual mais próximo. Esta definição não precisa mais de quantificadores e nem usa a epsilôntica de um limite. O princípio da transferência não significa que os números reais e hiperreais se comportem da mesma forma, apenas que não perdemos o que já sabemos. Por exemplo, ainda temos diferenciação, mas ##{}^*mathbb{R}## não é mais arquimediano. Da mesma forma, a configuração informal ##frac{1}{0}=infty ## é inválida, pois o princípio de transferência se aplica e zero não tem inverso multiplicativo. A contrapartida rigorosa de tal cálculo seria $$ dfrac{1}{varepsilon }= dfrac{omega }{1} textual content{ if }varepsilon neq 0 $$ onde ##varepsilon ## é um infinitesimal e ##omega ## um número infinito. Assim, o princípio de transferência de que precisamos para salvar o que já sabemos sobre análise também nos proíbe de transformar ##frac{1}{0}## em um número, mesmo no conjunto estendido de números hiperreais.
_____________
1) Detalhes sobre números hiperreais podem ser encontrados nas diversas versões linguísticas da Wikipédia ou pesquisando por “hiperreal” entre os artigos do Perception na PF.
