Formulário de interceptação de talude

Aprenda a escrever equações na forma de interceptação de inclinação: y = mx + b

Formulário de interceptação de inclinação: y = mx + b
onde m é a inclinação eb é a interceptação y

A forma de interceptação da inclinação de uma equação linear é y = mx + b, onde m é a inclinação eb é a interceptação y. O gráfico de uma equação linear é uma reta e y = mx + b é uma das formas mais comuns de escrever a equação de uma reta.

Como derivar a forma de interceptação de inclinação de uma equação linear

Considere um ponto arbitrário (x,y) na reta e um ponto (0,b) no eixo y. Então, você pode usar a fórmula de inclinação para derivar a forma de interceptação de inclinação.

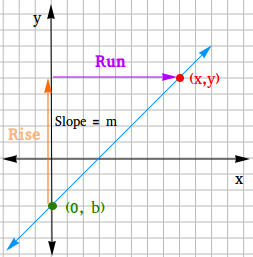
Inclinação = Ascender / Correr = (s₁ – sim₂) / (x₁ -x₂)

Usando (x₁sim₁) = (x,y) e (x₂sim₂) = (0,b), calcule a inclinação m.

m = (y – b) / (x – 0)

m = (y – b) / x

Multiplique ambos os lados da equação por x

(x)m = y – b

mx = y – b

Adicione b a ambos os lados da equação

mx + b = y – b + b

y = mx + b

Fórmula de interceptação de inclinação

Exemplos que mostram como encontrar a forma inclinação-interceptação de uma linha reta

O objetivo destes exercícios é escrever a equação de uma reta na forma inclinação-interseção (y = mx + b) considerando os seguintes casos:

• A inclinação e a interceptação y são fornecidas (exemplo #1)

• A inclinação e um ponto na linha são dados (exemplo #2)

• Dois pontos na reta são dados (exemplo #3)

Exemplo #1

Se a inclinação de uma linha for m = 2 e a interceptação em y for b = 5, escreva a forma de interceptação da inclinação da linha.

A equação é y = 2x + 5.

Exemplo #2

Se a inclinação de uma reta for m = 5 e (1, 6) for um ponto na reta, encontre a forma de interceptação da inclinação da reta.

Desta vez temos m, mas falta b, então temos que encontrar b.

Como m = 5, y = mx + b torna-se y = 5x + b.

Agora, use (1, 6) para obter b.

Como x = 1 e y = 6, você pode substituí-los na equação.

Substituindo 1 por x e 6 por y dá 6 = 5×1 + b.

6 = 5×1 + b é apenas um equação linear que você pode resolver para obter b.

6 = 5×1 + b

6 = 5 + b

Subtraia 5 de ambos os lados.

6 − 5 = 5 − 5 + b

1 = 0 + b

1 =b

Agora, como temos b, y = 5x + 1

Exemplo #3

Suponha que (2, 3) e (4, 9) sejam dois pontos em uma reta. Encontre a forma de interceptação da inclinação da linha.

Desta vez, m e b estão faltando, então a primeira coisa a fazer é obter m e então usar m e um ponto, (2, 3) ou (4, 9) para obter b.

Deixe x₁ = 4, você₁ = 9 e x₂ = 2, você₂ = 3

m = (s₁ − sim₂) / (x₁ −x₂) = (9 − 3) / (4 − 2 ) = 6/2 = 3

Agora podemos usar o valor de m e um ponto para obter b como já foi feito no exemplo #2.

Embora você tenha dois pontos, não importa qual ponto você escolhe. Como ambos os pontos estão na linha, eles produzirão resultados semelhantes.

Escolhendo (2, 3), x = 2 e y = 3

Substituindo 2 por x, 3 por y e 3 por m na equação y = mx + b, obtemos:

3 = 3 × 2 + b

3 = 6 + b

Subtraia 6 de ambos os lados

3 − 6 = 6 − 6 + b

-3 = 0 + b

-3 =b

Agora temos b = -3 e m = 3, y = 3x + -3

Casos Especiais de Formulário de Interceptação de Taludes

A interceptação y b é igual a zero

Neste caso, y = mx e a reta sempre passa pela origem do sistema de coordenadas.

A inclinação da reta é igual a zero

Neste caso, y = (0)x + b = be quando você representa graficamente a linha, ela será uma linha horizontal ao cruzar a interceptação y.

A inclinação da linha é indefinida

Neste caso, x é igual à coordenada x de qualquer ponto da reta ou qualquer outro número que lhe seja dado em um exercício. Quando você representa graficamente a linha, ela será uma linha vertical ao cruzar a interceptação x.