Se você já arrastou um baralho de cartas de jogo, provavelmente criou um baralho exclusivo. Ou seja, você provavelmente é a única pessoa que já organizou os cartões exatamente nessa ordem. Embora essa afirmação pareça incrível, é uma ótima ilustração da rapidez com que os números grandes podem surgir em situações cotidianas – com consequências ocasionalmente desafiadoras, como os desenvolvedores de um jogo de poker on -line descobriu dolorosamente no closing dos anos 90.
A matemática do traseiro de cartas é muito fácil de explicar. Para calcular quantos arranjos 52 cartas podem ter, você deve passar por todos os shuffles possíveis. Então, logicamente, uma das 52 cartas é colocada na parte superior e, uma vez que isso é determinado, existem apenas 51 possibilidades para o cartão abaixo dele. O próximo cartão tem apenas 50 opções possíveis e assim por diante. Um deck de 52 cartas pode, portanto, ser organizado em 52 × 51 × 50 × … × 2 × 1 = 52! maneiras diferentes.
Se você fizer a multiplicação e arredondar a resposta, receberá um número com 67 zeros. Isso é mais do que um quadrilhão vezes mais maneiras de organizar essas cartas do que os átomos na Terra.
Sobre apoiar o jornalismo científico
Se você está gostando deste artigo, considere apoiar nosso jornalismo premiado por assinando. Ao comprar uma assinatura, você está ajudando a garantir o futuro das histórias impactantes sobre as descobertas e idéias que moldam nosso mundo hoje.
Tão claramente existem muitas, muitas maneiras diferentes de organizar 52 cartas de jogo. E, no entanto, para descobrir a probabilidade de outra pessoa no mundo criar aleatoriamente a mesma sequência de cartas, não é suficiente para simplesmente calcular 1/52! Esse número simplesmente indica a probabilidade de obter uma embarcação muito específica de cartões.
Há uma pergunta mais sutil a considerar: qual a probabilidade de que duas ou mais pessoas no mundo embarquem aleatoriamente um baralho de cartas da mesma maneira?
A raridade extraordinária de cada shuffle
Esta questão é uma reminiscência do Paradoxo de aniversário. Funciona de acordo com o mesmo princípio: é improvável que um aluno de uma aula tenha um aniversário em uma determinada knowledge – em um grupo de 30 pessoas, a probabilidade disso é 1 – (364 /365)30≈ 7,9 %. A probabilidade de dois estudantes nascerem no mesmo dia é superior a 70 %, no entanto. A razão para essa aparente discrepância é que as pessoas geralmente subestimam quantos pares possíveis de estudantes existem. De 30 alunos, 435 pares podem ser formados. A probabilidade de que cada par de estudantes tenha nascido em um dia diferente, então não parece tão alto.
Se você deseja descobrir a probabilidade de embaralhar aleatoriamente um baralho de cartas da mesma maneira que qualquer outra pessoa no mundo, existem várias maneiras de fazê -lo. Primeiro, um é calcular a probabilidade do evento oposto e depois subtrair esse resultado de 1. Isso significa que você primeiro examina a probabilidade de que todas as pessoas do mundo criem um arranjo completamente novo ao misturar: a primeira pessoa tem uma probabilidade de 1, a segunda uma probabilidade de (52! – 1) / 52! Em seguida, subtraia este resultado de 1.
Se houver oito bilhões de pessoas no mundo, a probabilidade de várias pessoas criarem o mesmo embaralhamento de cartas podem ser calculadas da seguinte forma:
O problema é que minha calculadora (ou melhor, o programa on -line Wolfram | Alpha) falha quando tento avaliar essa fórmula. Portanto, tenho que confiar em uma estimativa muito aproximada dessa probabilidade:
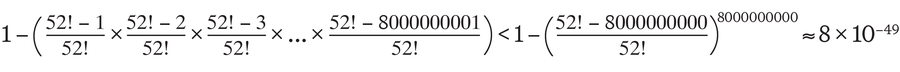
Isso significa que a probabilidade de que duas ou mais pessoas no mundo criem o mesmo baralho de cartas é inferior a 0,0000 … 08 % – um número que se desvia apenas de 0 no 47º lugar decimal.
Com essa ilustração, espero ter convencido a todos de que é extremamente improvável que várias pessoas no mundo criem aleatoriamente o mesmo baralho de cartas, embaralhando. Mas você provavelmente embaralhou as cartas muitas vezes em sua vida, não apenas uma vez. Então, como o resultado muda se assumirmos que cada pessoa embaralha aproximadamente 100 decks de cartas em sua vida? Ao substituir os oito bilhões na estimativa anterior por 800 bilhões, descobrimos que a probabilidade neste caso é menor que 8 × 10-43 por cento.
Em outras palavras, as possibilities não mudam muito. Mesmo que cada pessoa do mundo embaralhe um baralho de cartas 100 vezes, é muito improvável que o mesmo baralho apareça duas vezes.
Nesse caso, se considerarmos todas as pessoas que vive ou já haviam vivido na terra – algumas estimativas, sobre 117 bilhões Pessoas – cada uma das quais embaralhou um baralho de cartas cerca de 100 vezes (o que é improvável, já que nossa espécie não possui cartas de jogo há muito tempo), então a probabilidade de que o mesmo arranjo tenha sido criado várias vezes seja menor que 1,7 × 10-40 por cento.
Isso deixa claro: é realmente extremamente improvável que duas pessoas em toda a história da humanidade já tenham embarcado em um baralho de cartas da mesma maneira – pelo menos assumindo que elas embaralharam as cartas com muito cuidado. Isso ilustra o quão grande 52! é e quão enormemente muitas possibilidades existem para organizar 52 cartões.
Leia -os e chore
A vastidão de 52! Não é apenas inspirador para contemplar – ele também representou alguns problemas práticos significativos para os desenvolvedores de jogos on -line. O poker on -line pode envolver grandes somas de dinheiro, por isso é elementary que esses jogos sejam o mais seguros e justos possível. Quaisquer falhas ou brechas podem ser exploradas por trapaceiros ou usadas pela casa contra jogadores.
Os cartões digitais devem ser bem embaralhados e tratados aleatoriamente, assim como os reais. Em um mundo perfect, um algoritmo selecionaria aleatoriamente um arranjo do 52! decks possíveis. Mas nenhum computador tem memória suficiente para avaliar todas essas possibilidades, e um gerador de números aleatórios perfeito ainda não existe. Portanto, os desenvolvedores geralmente dependem de algoritmos que simulam o embaralhamento do cartão.
No closing dos anos 90, a plataforma de desenvolvimento ASF Software program forneceu vários provedores de poker on-line, como o Planet Poker, com algoritmos de abafamento de cartões. A plataforma até postou o algoritmo em seu web site como prova de que o jogo foi programado de maneira confiável. E este put up chamou a atenção de alguns funcionários da Confiable Software program Applied sciences, uma empresa de TI. “Assim que vimos o algoritmo de embaralhamento, começamos a suspeitar que pode haver um problema. Uma pequena investigação provou que essa intuição estava correta”, alguns funcionários escreveu em um put upem um web site de desenvolvimento de software program.
O algoritmo começou com um baralho ordenado de cartas e depois trocou duas cartas por vez em várias etapas. Para fazer isso, o programa usou um gerador de números aleatórios vinculado ao tempo do sistema do computador. Mas existem várias restrições nesse método. Por um lado, o mecanismo de troca foi implementado de modo que certos acordos de cartão eram favorecidos e mais propensos a aparecer do que outros. Por outro lado, o sistema vincula sua geração de números ao número de segundos que passaram desde meia -noite, redefinindo uma vez por dia, o que limita ainda mais os possíveis valores aleatórios. Apenas cerca de 86 milhões de acordos poderiam ser gerados dessa maneira, descobriu a equipe de tecnologias de software program confiável.
Os programadores perceberam que, como o sistema está vinculado a um relógio para randomizar seus shuffles, o arranjo dos cartões poderia ser ainda mais restrito, levando em consideração esse cronometrista. Simplesmente sincronizar seu próprio programa com o relógio do sistema reduziu as possibilidades a meros 200.000 decks em potencial que o algoritmo poderia gerar. “Após esse movimento, o sistema é nosso, uma vez que procurar esse pequeno conjunto de shuffles é trivial e pode ser feito em um PC em tempo actual”, eles escreveram. Lembre -se de que isso foi nos anos 90, quando os computadores eram significativamente menos poderosos do que são hoje.
Os funcionários de tecnologias de software program confiáveis relataram essas fraquezas aos desenvolvedores do algoritmo, que o revisaram imediatamente. Hoje, muitos websites de pôquer on -line usam o algoritmo Fisher -Yates, também chamado de Knuth Shuffle (que soa deliciosamente como uma dança). É fácil implementar e fornecer resultados satisfatórios.
Obviamente, esses algoritmos são limitados de outras maneiras – os geradores random simplesmente não são bons o suficiente para fazer o que as pessoas podem fazer com um baralho actual. Mas mesmo o traficante humano mais hábil não pode fornecer uma mão perfeita sempre.
Graças ao podcast da língua alemã Nerds no trabalho Podcast por me inspirar a escrever sobre esse algoritmo de poker dos anos 90.
Este artigo apareceu originalmente em Spektrum der Wissenschaft e foi reproduzido com permissão.






