Introdução: “NOTAÇÃO Conveniente”
Em Dirac’s Princípios da mecânica quântica Publicado em 1930, ele introduziu uma “notação conveniente” que ele chamou de “função delta” que ele tratou como um análogo contínuo ao discreto Delta do Kronecker. O Delta do Kronecker é simplesmente os componentes indexados do operador de identidade na álgebra matricial:
(tex) delta^j_k = left { Start {Array} {lcl} 1 & textual content {if} & j = okay 0 & textual content {if} e j ne okay finish {Array} dight. (/tex)
A principal utilidade do Delta do Kronecker é sua ocorrência nas sumaturas:
(tex) a_k = sum_ {j = 1} ^n a_j delta ^j_k (/tex)
Da mesma forma, a função delta da Dirac é definida principalmente como ocorre nas integrais:
(tex) f (y) = int _ {- infty}^{ infty} f (x) delta (xy) dx. (/tex)
Visto de outra maneira como a função delta permite avaliar a função em zero (e, by way of traduções, em outros lugares) integrando:
(tex) f (0) = int _ {- infty}^ infty f (x) delta (x) dx (/tex)
O problema é que não existe essa função, como tal, no espaço das funções reais. A “função” delta não é, de fato, uma função e é por isso que Dirac se referiu a ela como “notação conveniente”.
Isso levanta a questão: “Então o que isso faz notação conveniente representar? ” Para o matemático, isso significa “Onde está o rigor? ” E para o físico significa “Usar isso me dará previsões bem definidas? ” Este artigo aponta para alguns dos contextos matemáticos em que a notação conveniente de Dirac recebeu um significado matemático adequado.
Riemann-Stieltjes integrais
Podemos definir formalmente o Riemann-Stieltjes (RS) integral:
(tex) int_a^bf (x) dg (x) (/tex)
Para funções reais bem comportadas (ITEX) F (/ITEX) e (ITEX) G (/ITEX) da mesma maneira que definimos nossas integrais de Riemann, como os limites de Riemann (modificados) somos. Onde (Itex) G (/ITEX) é diferenciável, também podemos provar a integração por peças mantém e expressar essas integrais de RS como integrais simples de Riemann:
(tex) int_a^bf (x) dg (x) = esquerda. f (x) g (x) direita rvert_a^b – int_a^bg (x) df (x) = esquerda. f (x) g (x) proper rvert_a^b – int_a^b f ‘(x) g (x) dx, (/tex)
Isso é válido mesmo quando o derivado de (ITEX) g (/iTex) é problemático no intervalo de integração.
É claro que as identidades são ruas bidirecionais e reescrevemos as integrais aparentes de Riemann, bem como as integrais RS definidas.
Esta é uma melhoria, porque as integrais de Reimann-Stieltjes têm um domínio mais amplo de aplicação.
A função do Delta Dirac como a “derivada” da função da etapa Heaviside
Considere a função (itex) theta (/itex) de modo que:
(tex) theta (x) = esquerda { Start {Array} {rcl} 1 & textual content {if} & x ge 0 0 & textual content {if} & x <0 finish {Array} (/tex)
Esta é a função de etapa da Heaviside, que também é denotada (ITEX) H (x) (/iTex) em muitos textos.
Agora considere o RS integral:
(tex) i = int_a^bf (x) d theta (x) quad a, b ne 0. (/tex)
A avaliação cuidadosa do limite da soma Riemann modificada produzirá zero se (Itex) 0 (/iTex) estiver fora do intervalo aberto (ITEX) (a, b) (/iTex). Mas para (itex) a <0
(tex) f (c) = int_a^bf (x) d theta (xc) (/tex)
Assim, obtemos exatamente o mesmo comportamento que a “notação conveniente” de Dirac e podemos usar isso como o definição dessa notação:
(tex) int_a^bf (x) delta (x) dx equiv int_a^bf (x) d theta (x). (/tex)
Portanto, frequentemente falamos da função Delta do Dirac como o “derivado” da função da etapa Heaviside.
No entanto, o uso de integrais de RS não lida diretamente com outras notações igualmente convenientes. Por exemplo, podemos considerar “derivados” da função delta do Dirac (ITEX) delta^{(n)} (/iTex) que têm a propriedade definidora de avaliar o derivado n-és
(tex) int _ {- infty}^ infty f (x) delta^{(n)} (x) dx equiv (-1)^nf^{(n)} (0). (/tex)
Pode-se obter esse resultado aplicando repetidamente a integração por peças para retirar os derivados formais de (Itex) delta (/iTex) até que alguém tenha uma integral válida de Riemann-Stieltjes. Isso sugere que podemos estender a definição, digamos Estendido Riemann-Stieltjes itegraals. No entanto, essa abordagem agora foi suplantada com a integração de Lebesgue e a função delta de Dirac é considerada (notação para) um distribuição. Especificamente, é (e seus derivados são) expresso em termos da derivada (s) de Radon-Nikodym da medida definida pela função da etapa Heaviside.
Há mais operacional Abordagem para entender a função delta da Dirac em termos de como ela está realmente sendo usada.
Vetores, vetores duplos e teorema da representação de Riesz
Lembre -se de que, para os espaços vectoros dimensionais finitos, digamos ## v ## o conjunto de funcionais lineares (mapeamentos lineares de vetores para escalares) forma seu próprio espaço vetorial, o espaço duplo ## v^*## de dimensão igual. Para espaços dimensionais infinitos, esse também é o caso, exceto a dimensão do espaço duplo pode ser uma ordem mais alta de infinito. Isso entra em jogo quando o espaço vetorial também possui um Produto interno (por exemplo, o produto DOT) nesse caso a representação Riesz se aplica.
Teorema da representação de Riesz: Para qualquer espaço vetorial ## v ## com produto interno ## langle cdot, cdot rangle ##, para cada Funcional linear limitado ## varphi ## existe um vetor ## mathbf {u} ## tal que:
(tex) varphi ( mathbf {v}) = langle mathbf {u}, mathbf {v} rangle (/tex) (nós usamos aqui a convenção que os produtos internos complexos são lineares no 2º argumento, quando muitos textos revertem isso. alpha, beta rangle = langle beta, alpha rangle^*= langle beta^*, alpha^* rangle ##.)
Agora, se estivermos trabalhando em espaços vetores reais, o produto interno é essencialmente um “produto de ponto”, para que possamos dizer que identificamos o funcional linear limitado ## varphi ## com a operação ## mathbf {u} bullet ##, de notar o vetor de argumento com ## mathbf {u}}.
Um funcional linear limitado (em um espaço interno do produto) é um funcional como seu valor absoluto é limitado sobre o conjunto de vetores com norma unitária. Para espaços de dimensão finita, esse é sempre o caso. Essa condição de limitação é algo com o qual só precisamos nos preocupar em espaços infinitos-dimensionais.
Por causa desse teorema, ao ensinar vetores introdutórios e álgebra linear, não há necessidade pragmática de criar espaços duplos. É suficiente para expressar qualquer operação de vetor duplo em termos de um vetor e produto de ponto.
Os problemas ocorrem quando precisamos ir além dos espaços dimensionais finitos. Em seguida, precisamos lidar com esses funcionais lineares ilimitados explicitamente quando são usados.
O “produto dot” de duas funções
Agora considere o espaço vetorial de todas as funções de valor actual. Para implementar um produto interno e Norm, precisamos restringir a um subespaço onde essas operações são finitas, mas podemos encobrir esses detalhes para esta discussão. Definimos o seguinte produto interno (DOT) entre dois vetores adequados:
(tex) f bullet g = int _ {- infty}^ infty f (x) g (x) dx (/tex)
Observe que, com um produto interno, também temos uma norma e, portanto, podemos normalizar nossas funções (construir “vetores da unidade”).
(tex) lvert f rvert = sqrt {f bullet f} = sqrt { int _ {- infty}^ infty f^2 (x) dx} (/tex)
Por exemplo, para (itex) f (x) = frac {1} {x^2+1} (/itex) e (itex) g (x) = e^{-x^2/2} (/itex) que temos:
(tex) f bullet g = int _ {- infty}^ infty e^{-x^2/2} frac {1} {x^2+1} dx aprox 1.64354 (/tex)
e
(tex) lvert f rvert = sqrt { int _ {- infty}^ infty (e^{-x^2/2})^2 dx} = sqrt (4) { pi} aprox 1.3313 (/tex)
Portanto, (Itex) hat {f} (x) = frac {1} { sqrt (4) { pi}} f (x) (/iTex) é um função normalizada ou seja, um “vetor de unidade” neste espaço (itex) l^2 (/itex).
Para muitas funções, a integral que definir sua norma divergirá ou simplesmente não pode ser definida. Então, jogamos esses casos e restringimos nossas considerações às funções definidas da norma finita. Isso novamente outline um espaço vetorial(iTex) l^2 ( mathbb {r}) (/iTex) O espaço das funções integráveis quadradas. Como a norma é definida em termos de um produto interno, este é um Espaço de produto interno.
A avaliação funcional
Infelizmente, para ilimitado Funcionais lineares O teorema da representação de Riesz falha. Pode -se pensar que isso não é muito importante. Mas ficará surpreso ao ver com que frequência uma operação importante envolve um funcional linear que é ilimitado.
Podemos definir o conjunto de funcionais de avaliação, (Itex) e_a, a in mathbb {r} (/iTex) tal que (iTex) e_a (f) = f (a) (/itex).
- Eles são funcionais na medida em que mapeiam funções para números.
- Que eles são linear é trivial:
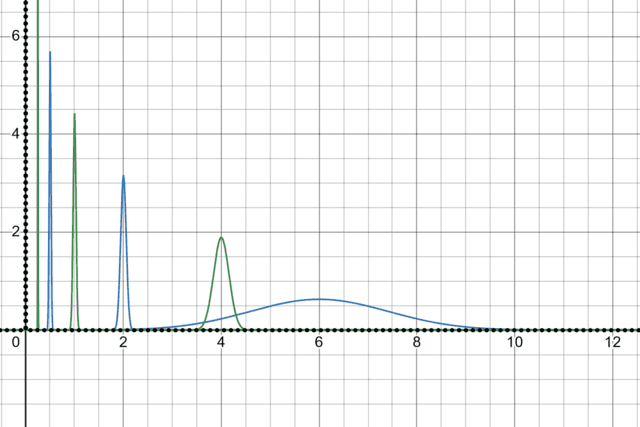
(tex) e_a ( alpha f+ beta g) = alpha f (a)+ beta g (a) = alpha e_a (f)+ beta e_a (g) (/tex) - Que eles são ilimitado (IN (ITEX) l^2 (s) (/iTex)) é bastante fácil de demonstrar. Por exemplo, em (Itex) l^2 ( mathbb {r}) (/iTex) A raiz quadrada da função de densidade de probabilidade para uma variável aleatória regular possui norma unitária, (ITEX) 1 (/ITEX) (a probabilidade whole).
À medida que o desvio padrão se aproxima, a densidade de probabilidade na média se aproxima do infinito. A avaliação na média é, portanto, uma funcional linear ilimitada.
Assim, a forma contrapositiva do teorema da representação de Riesz diz que não há função (iTex) phi (/iTex), de modo que:
(tex) e_a (f) = int _ {- infty}^ infty phi (x) f (x) dx. (/tex)
Mas nós podemos fingir que existe definindo o notação conveniente:
(tex) int _ {- infty}^ infty delta (xa) f (x) dx equiv e_a (f) = f (a) (/tex)
A avaliação está no centro do que queremos dizer com funções. A função Delta Dirac e seus derivados (literais e figurativos) são, portanto, extremamente úteis notação conveniente. Portanto, sairemos deste buraco de coelho aqui, embora haja muito mais que possamos explorar. Espero que essa exposição possa fornecer alguma inspiração para explorar questões semelhantes, como “O que é uma função de onda? ” e “O que é um campo? ”.