O cubóide é uma caixa sólida cuja superfície é um retângulo da mesma área ou áreas diferentes.
UM cubóide terá um comprimentoAssim, largura e altura.
Portanto, podemos concluir que o quantity é tridimensional. Para medir os volumes, precisamos conhecer a medida 3 lados.
Como o quantity envolve 3 lados, é medido em unidades cúbicas.
Quantity de um cubóide = (comprimento × largura × altura) unidades cúbicas.
= (L × B × H) unidades cúbicas.
(Desde área = ℓ × b)
Quantity de um cubóide = área de uma superfície × altura unidades cúbicas
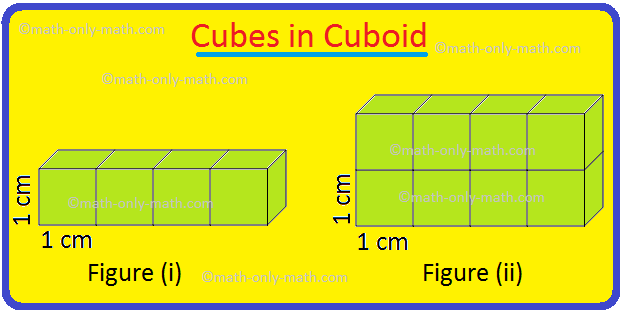
1. Vejamos o cubóide dado.
O comprimento do cubóide = 5 cm
A amplitude do cubóide = 3 cm
A altura do cubóide (espessura) = 2 cm
O número de 1 cm de cubos no cubóide dado = 30 cubos = 5 × 3 × 2
Descobrimos que o quantity do cubóide fornecido com comprimento 5 cm, largura 3 cm e altura 2 cm é de 30 cu cm.
Portanto, quantity de um cubóide = comprimento × largura × altura
Um cubóide é uma figura sólida com comprimento, largura e altura. É um sólido retangular.
2. Na figura, vemos um sólido retangular cujo comprimento é de 5 cm, a largura é de 3 cm e a altura é de 3 cm.
Para encontrar seu quantity, dividimos -o em cubos de unidade de 1 cm.
Descobrimos que a camada superior contém 5 × 3 = 15 cubos.
O número whole dessas camadas é 3.
Então, o whole de cubos é 15 × 3 = 45
Então, o quantity deste cubóide é de 45 cm3 Porque o quantity de cada cubo é 1 cm cúbico ou 1 cm3
Quantity de um cubóide = comprimento × largura × altura
v = ℓ × b × h
Por exemplo, no caso acima,
ℓ = 5 cm
b = 3 cm e
h = 3 cm
Portanto, o quantity do cubóide dado = (5 × 3 × 3) cm³ = 45 cm³
Problemas de palavras no quantity de um cubóide
Exemplos resolvidos no quantity de um cubóide:
1. Encontre o quantity de um cubóide de dimensões 14 cm × 12 cm × 8 cm.
Solução:
Quantity de cubóide = comprimento × largura × altura.
Aqui, comprimento = 14 cm, largura = 12 cm e altura = 8 cm.
Quantity de cubóide = 14 × 12 × 8 cm cúbico.
= 1344 cm cúbico.
Portanto, quantity de cubóide = 1344 cm cúbico.
2. Michael fez uma caixa de sapatos com comprimento 8 cm, largura 6 cm e altura 6 cm. Encontre o quantity da caixa.
Solução:
Quantity da caixa de sapatos = comprimento × largura × altura.
= 8 × 6 × 6
= 288 cu cm.
3. Um tanque de peixes tem 40 cm de comprimento, 15 cm de largura e 10 cm de altura. Qual é o seu quantity no CU CM?
Solução:
O comprimento do tanque de peixes = 40 cm
A amplitude do tanque de peixes = 15 cm
A altura do tanque de peixes = 10 cm
Portanto, o quantity do tanque de peixes = comprimento × largura × altura.
= 40 × 15 × 10 cu. cm
= 6000 cu cm.
4. Encontre o quantity de um cubóide de dimensões 14 cm × 50 mm × 10 cm.
Solução:
Aqui, comprimento = 14 cm,
(Dada, largura = 50 mm; precisamos converter largura na mesma unidade e depois resolver. Sabemos, 10 mm = 1 cm. Portanto, 50 mm = 50/10 cm = 5 cm).
Largura = 5 cm,
Altura = 10 cm.
Quantity de cubóide = comprimento × largura × altura.
= 14 × 5 × 10
= 700 cm cúbicos.
Portanto, quantity de cubóide = 700 cm cúbico.
Observação: Em um cubóide, quando o comprimento, a largura e a altura são de unidades diferentes, convertem -as em uma mesma unidade e depois resolvam.
5. Encontre o quantity de um cubóide de dimensões 17 mm × 0,2 cm × 12 mm em Cu. cm.
Solução:
Dado, comprimento = 17 mm.
Sabemos, 10 mm = 1 cm.
= 17/10 cm.
= 1,7 cm.
Portanto, comprimento = 1,7 cm.
Da mesma forma, altura = 12 mm.
Sabemos, 10 mm = 1 cm.
= 12/10 cm.
= 1,2 cm.
Portanto, altura = 1,2 cm.
Quantity de cubóide = comprimento × largura × altura.
Comprimento = 1,7 cm, largura = 0,2 cm e altura = 1,2 cm.
= 1,7 × 0,2 × 1,2 cu. cm.
= 0,408 cu. cm.
Portanto, quantity de cubóide = 0,408 cm cúbico.
6. Encontre o número de caixas cúbicas do lado cúbico 3 cm, que podem ser acomodadas na caixa de dimensões 15 cm × 9 cm × 12 cm.
Solução:
Quantity de caixa = lateral × lateral × lado.
= 3 × 3 × 3
= 27 cu. cm.
Quantity de caixa = comprimento × largura × altura.
= 15 × 9 × 12
= 1620 Cu. cm.
Número de caixas = quantity de caixa/quantity de cada caixa.
= 1620/27
= 60
Portanto, número de caixas cúbicas = 60.
7. Quantos tijolos cada um de 25 cm de comprimento, 10 cm de largura e 7,5 cm de espessura serão necessários para uma parede de 20 m de comprimento, 2 m de altura e 0,75 m de espessura? Se os tijolos venderem a US $ 900 por mil, o que custará para construir a parede?
Solução:
Quantity da parede = 20 m × 2 m × 0,75 m
= 20 × 100 cm × 2 × 100 cm × 0,75 × 100 cm
Quantity de tijolo = 25 cm × 10 cm × 7,5 cm
Número de tijolos = ( frac { textrm {quantity da parede}} { textrm {quantity do tijolo}} )
= ( frac {20 × 100 × 2 × 100 × 0,75 × 100} {25 × 10 × 7,5} )
= 16000
O número de tijolos = 16000
O custo de 1 mil tijolos = $ 900
O custo de construção da parede = $ 900 × 16 = $ 14400
Observação: Ao calcular o quantity de um cubóide, todas as dimensões devem ser alteradas para a mesma unidade.
8. Encontre o quantity de um tanque cuboidal cujo comprimento, largura e altura são 10 m, 8 m e 5 m, respectivamente.
Solução:
Comprimento de tanque cuboidal = 10 m
Largura de tanque cuboidal = 5 m
Altura do tanque cuboidal = 8 m
Quantity de tanque cuboidal = comprimento × largura × altura
= 10 m × 8 m × 5 m
= 400 m3
Planilha sobre quantity de um cubóide
Perguntas e respostas sobre cubóides:
1. Encontre o quantity de cada um dos cubóides.
(i) Comprimento = 5 cm, largura = 4 cm e altura = 3 cm
(ii) Comprimento = 15 m, largura = 10 me altura = 2 m
(iii) comprimento = 0,5 m, largura = 3 me altura = 4 m
(iv) Comprimento = 3,2 cm, largura = 2 cm e altura = 8 cm
(v) comprimento = 5 m, largura = 1,5 me altura = 1,2 m
Respostas:
1. (i) 60 cu. cm
(ii) 300 cu. m
(iii) 6 cu. m
(iv) 51,2 cu. cm
(v) 9 cu. m
2. Encontre o quantity desses tanques.
(i) Comprimento = 16 cm, largura = 60 cm e altura = 20 cm
(ii) comprimento = 6 m, largura = 3 me altura = 5 m
(iii) Comprimento = 2 m, largura = 1,5 me altura = 1,5 m
(iv) Comprimento = 80 cm, largura = 20 cm e altura = 40 cm
(v) Comprimento = 1,2 m, largura = 1,2 me altura = 1 m
Respostas:
2. (i) 19200 cu. cm
(ii) 90 cu. m
(iii) 4,5 cu. m
(iv) 64.000 cu. cm
(v) 1,44 cu. m
3. Encontre o quantity de cubóides com as seguintes medidas.
|
Comprimento |
Largura |
Altura |
|
|
(eu) |
8,5 cm |
6 cm |
3 cm |
|
(ii) |
14 cm |
11 cm |
9 cm |
|
(iii) |
30,5 cm |
25 cm |
20 cm |
|
(4) |
15,5 m |
12 m |
8 m |
|
(v) |
7 m |
4 m |
4 m |
Respostas:
3. (i) 153 cm3
(ii) 1368 cm3
(iii) 15250 cm3
(iv) 1488 m3
(v) 112 m3
Problemas de matemática da 5ª série
Do quantity de um cubóide para a página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.