Construção de um círculo | Regras de trabalho

Um círculo é uma coleção de todos esses pontos em um plano cuja distância de um ponto fixo permanece constante.

Centro: O ponto fixo no plano que é equidistante de todos os pontos do limite de um círculo é chamado de centro.

Na figura, O é o centro do círculo.

Raio: A distância fixa entre o centro e qualquer ponto no limite do círculo é chamada raio.

Na figura, o boi é um raio.

Acorde: Um segmento de linha que une dois pontos em um círculo é chamado de acorde do círculo.

Na figura, Mn é um acorde.

Diâmetro: Um acorde que passa pelo centro de um círculo é chamado de diâmetro do círculo.

Na figura, Yz é um diâmetro. O comprimento de um diâmetro = 2 × raio.

Em um círculo, o diâmetro é o acorde mais longo.

Construção de um círculo quando o comprimento de seu raio é dado:

Regras de trabalho para a construção de um círculo:

Passo I: Abra a bússola de modo que seu ponteiro seja colocado no ponto inicial (ou seja, O) da régua / escala e a extremidade do lápis seja colocada em uma marca, digamos 3 cm (que o raio do círculo seja 3 cm).

Etapa II: Marque um ponto com lápis, onde queremos o centro do círculo: deixe ser O.

Etapa III: Coloque o ponteiro da bússola em o que marcamos na etapa II.

Etapa IV: Vire a bússola ao redor do ponto O para obter o círculo necessário.

Construindo um círculo:

Desenhamos um círculo com a ajuda de um par de bússolas, fornecido na caixa de geometria e um lápis fino.

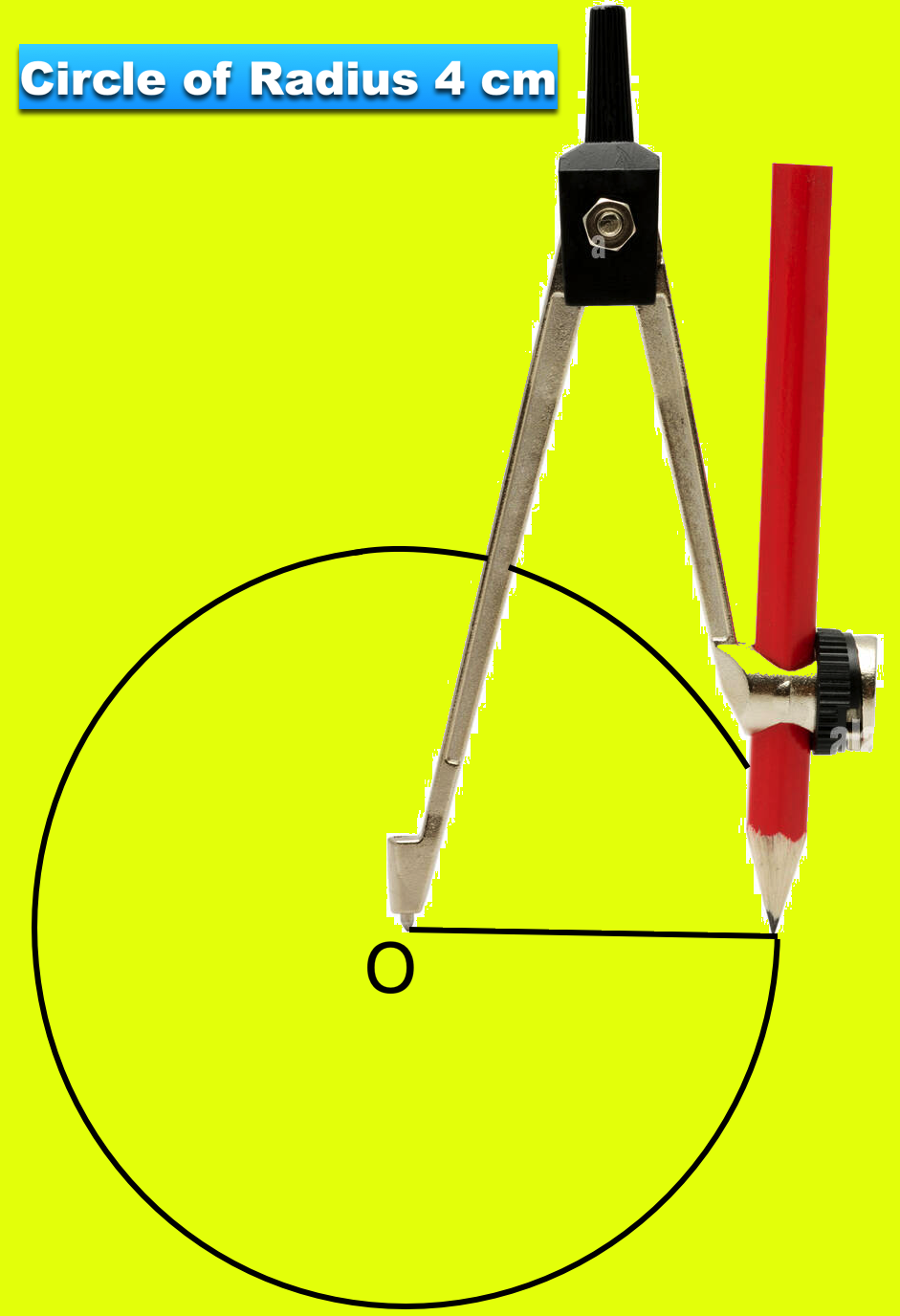
Vamos desenhar um círculo de raio 4 cm. Observamos as seguintes etapas.

Passo I: Expandimos os dois braços de um par de bússolas e tomamos a medida de 4 cm na escala, colocando a extremidade pontiaguda em zero e a outra extremidade com um lápis a 4 cm, marca na escala, como mostrado na figura.

Etapa II: Tomamos um ponto conveniente o em um pedaço de papel.

Etapa III: Corrigimos a extremidade pontiaguda do par de bússolas em O e movimentamos o ponto de lápis em torno de segurar o par de bússolas firmemente no topo. Temos a forma redonda desejada chamada círculo.

Exemplo de construção de um círculo:

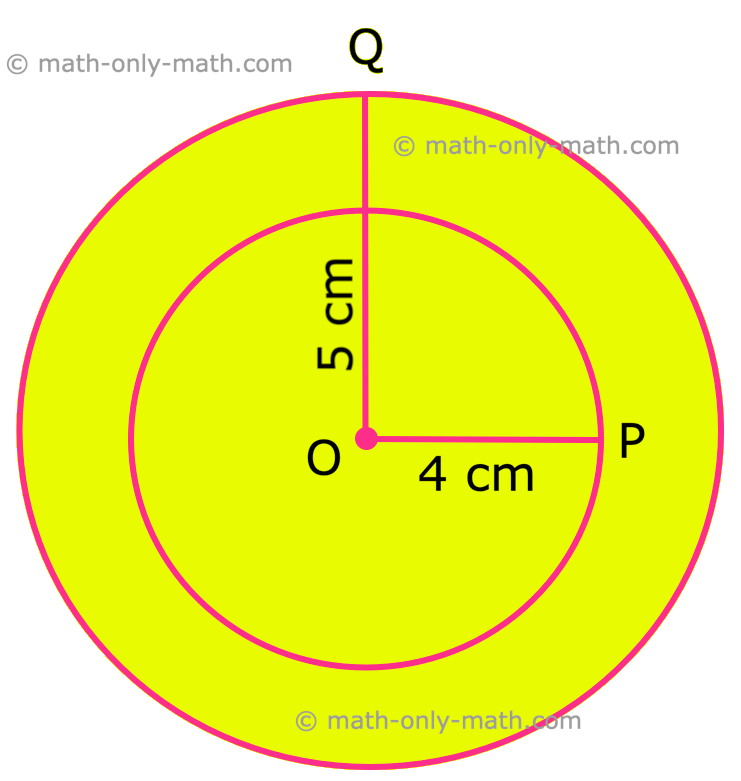
1. Desenhe dois círculos de raios de 4 cm e 5 cm com o mesmo centro O.

EU. Abra a bússola colocando o ponteiro no ponto inicial de uma escala e abrindo a extremidade de lápis até 5 cm.

Ii. Marka Level O com lápis e considere -o como centro do círculo.

Iii. Coloque o ponteiro da bússola em O.

4. Vire a bússola em O para obter o círculo de raio 5 cm.

V. Com a ajuda das mesmas etapas acima, desenhe um outro círculo de raio 4 cm com o mesmo o centro.

Exemplo resolvido no círculo:

1. Encontre o raio do círculo cujo diâmetro é de 28 cm.

Solução:

Raio de um círculo = ( frac { textrm {diâmetro do círculo}} { textrm {2}} )

= ( frac {28} {2} ) cm

= 14 cm

Planilha sobre a construção de um círculo:

1. Perguntas de múltipla escolha (MCQ) no círculo:

Marcação (✔) a opção correta.

(i) O raio de um círculo de diâmetro 20 cm é

(a) 8 cm

(b) 10 cm

(c) 4,0 cm

(d) 4,5 cm

(ii) encontre o diâmetro do círculo quando o raio estiver

(a) 3,8 cm

(b) 7,3 cm

(c) 2,9 cm

(d) 4,8 cm

(iii) O é o centro de um círculo e seu raio é de 5 cm. Onde está P, quando

(i) OP = 5,2 cm?

(ii) op ​​= 5cm?

(iii) OP = 4,8 cm?

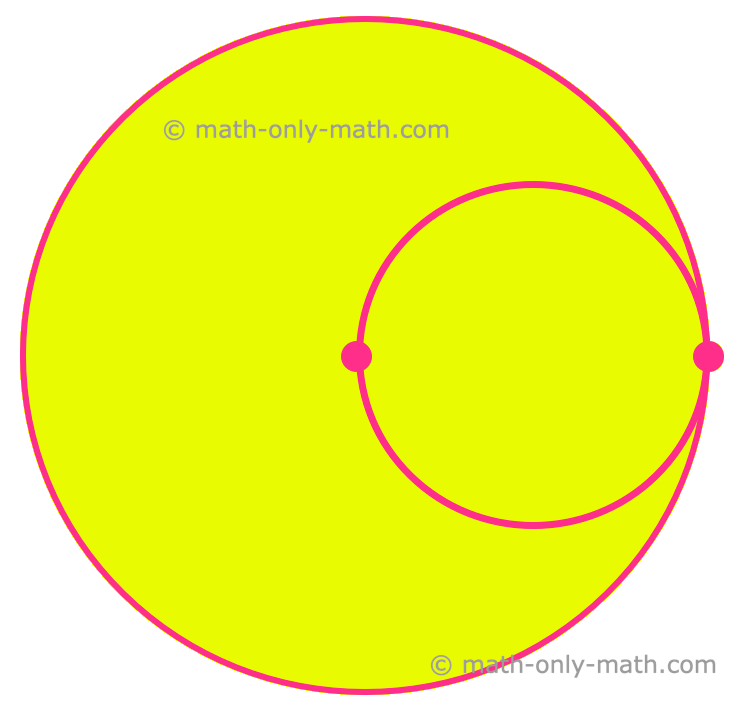
4. Desenhe dois círculos, um com raio 6 cm e outro com 3 cm, como mostrado na figura a seguir, de modo que o círculo interno passe pelo centro do outro círculo.

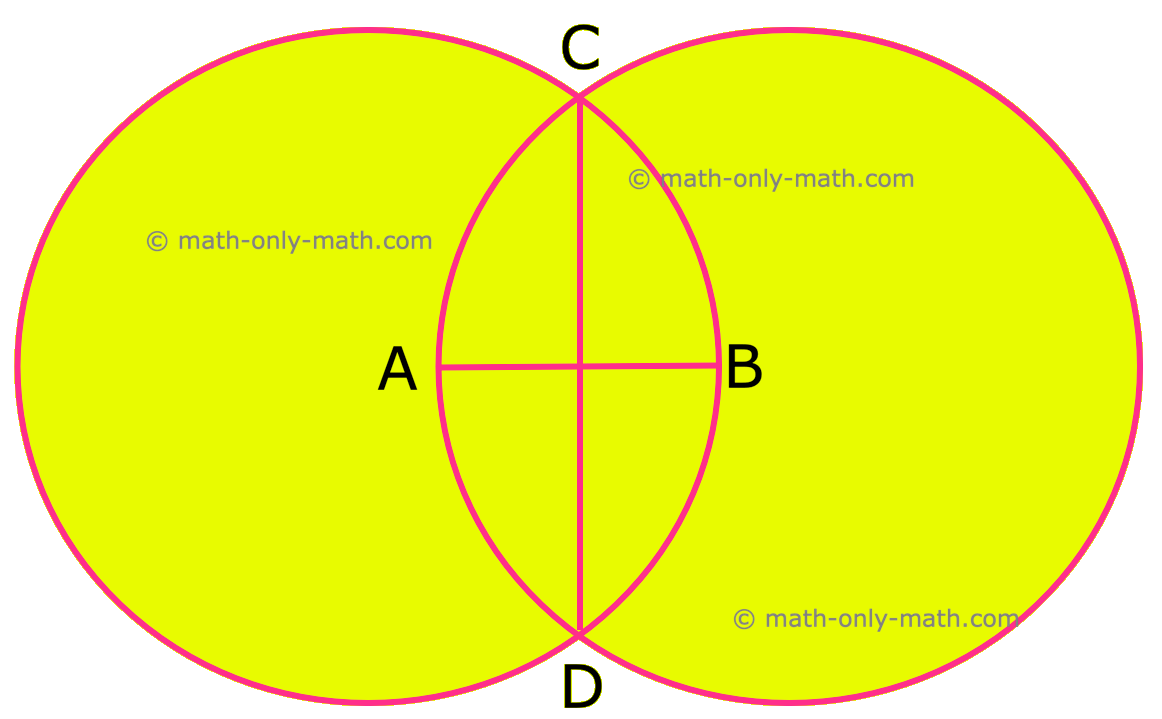
5. Desenhe dois círculos de raios iguais com os centros A e B, de modo que cada um deles passe pelo centro do outro. Verifique se AB ⊥ CD.

6. Com o mesmo centro O, desenhe três círculos de raios de 2,5 cm, 3,5 cm e 4,5 cm.

Problemas de matemática da 7ª série

Prática matemática da 8ª série

Da construção de um círculo à página inicial