Assine o nosso Canal do youtubePara os vídeos, atualizações e dicas mais recentes.
Discutiremos aqui algumas das propriedades do triângulo.
I. Propriedade do ângulo Soma de um triângulo:
Relação entre as medidas de três ângulos de um triângulo.
A soma de três ângulos de cada triângulo é de 180 °.
Em ∆ABC, Ero + porteb + ero = 180 °,
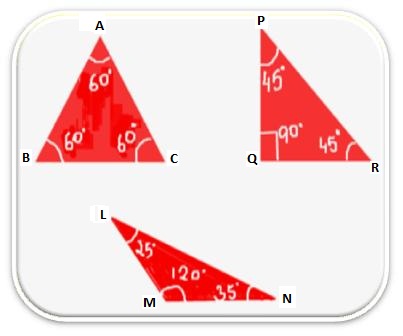
Desenhe três triângulos no seu livro não. Nomeie -os como ∆PQR, ∆ABC e ∆lmn. Com a ajuda do protetor, medem todos os ângulos dos ângulos e os encontre:
Em ∆ABC
EroBC + eroBCA + eroCAB = 180 °
Em ∆Pqr
EroPqr + porte QRP + porterpq = 180 °
Em ∆lmn
Portelmn + mnl + portenlm = 180 °
Aqui, observamos que, em cada caso, a soma das medidas de três ângulos de um triângulo é de 180 °.
Por isso, o A soma dos três ângulos de um triângulo é igual a 180 °.
Observação: Se dois ângulos de um triângulo forem dados, podemos facilmente descobrir seu terceiro ângulo.
Exemplos resolvidos em propriedade de um triângulo de ângulo de um triângulo:
1. Em um triângulo direito, se um ângulo for de 50 °, encontre seu terceiro ângulo.
Solução:
∆ PQR é um triângulo certo, ou seja, um ângulo é o ângulo certo.
Dado, eroPQR = 90 °
EroQpr = 50 °
Portanto, eroQrp = 180 ° – (eroq + porte p)
= 180 ° – (90 ° + 50 °)
= 180 ° – 140 °
ϨR = 40 °
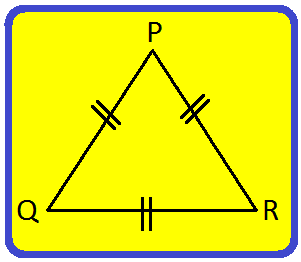
2. O PQR é um triângulo equilátero. Encontre a medida de cada ângulo.
Solução:
O PQR é um triângulo equilátero.
EroP = eroQ = ero
De acordo com a propriedade do ângulo de um triângulo, temos
Portanto, cada ângulo de um triângulo equilátero é de 60 °.
Ii. Propriedade da desigualdade do triângulo:
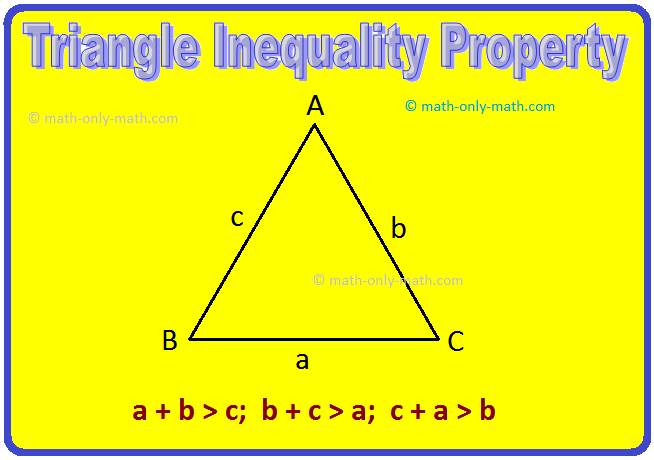
Propriedade da desigualdade do triângulo é a relação entre os comprimentos do lado de um triângulo.
∆ABC tem três lados, a saber, BC e CA.
Para uma notação mais curta, o comprimento do lado oposto ao vértice a é escrito como ‘a’
ou seja, a = bc
Da mesma forma, B = Ca e C = AB
Se medirmos os comprimentos de A, B e C, encontramos a seguinte relação:
a + b> c
B + C> A
c + a> b
Agora, temos o seguinte:
A soma de dois lados em um triângulo é maior que o terceiro lado.
Exemplos resolvidos em propriedades de desigualdade de triângulo:
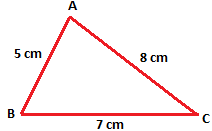
1. Desenhe um ∆ABC. Meça o comprimento de seus três lados.
Deixe os comprimentos dos três lados serem AB = 5 cm, BC = 7 cm, CA = 8 cm.
Agora adicione os comprimentos de dois lados examine essa soma com os comprimentos do terceiro lado.
(eu) AB + BC = 5 cm + 7 cm = 12 cm
Desde 12 cm> 8 cm
Portanto, (AB + BC)> AC
(ii) BC + CA = 7 cm + 8 cm = 15 cm
Desde 15 cm> 5 cm
Portanto, (BC + CA)> AB
(iii) Ca + AB = 8 cm + 5 cm = 13 cm
Desde 13 cm> 7 cm
Portanto, (CA + AB)> BC
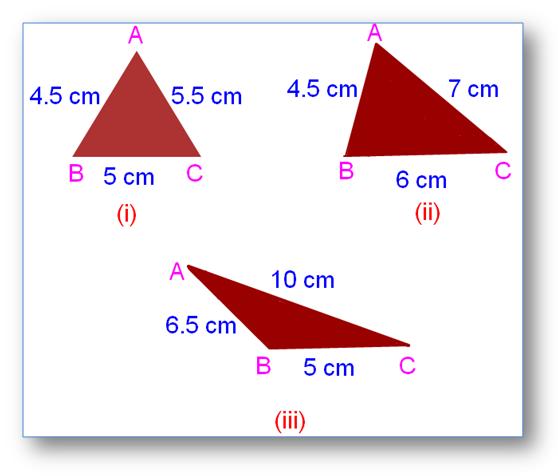
Na figura abaixo, podemos ver em cada caso, se somarmos dois lados do ∆, a soma é superior ao seu terceiro lado.
Assim, concluímos que a soma do comprimento de dois lados de um triângulo é maior que o comprimento do terceiro lado.
Exemplos resolvidos em propriedades de desigualdade de triângulo:
1. É possível ter um triângulo cujos lados são 5 cm, 6 cm e 4 cm?
Solução:
Os comprimentos dos lados são 5 cm, 6 cm, 4 cm,
(a) 5 cm + 6 cm> 4 cm.
(b) 6 cm + 4 cm> 5 cm.
(c) 5 cm + 4 cm> 6 cm.
Portanto, é possível um triângulo com esses lados.
2. Qual das alternativas a seguir pode ser o possível comprimento (em cm) de um triângulo?
(i) 3, 5, 3
(ii) 4, 3, 8
Solução:
(i) Como 3 + 5 (ou seja, 8)> 3, 5 + 3 (ou seja, 8)> 3 e 3 + 3 (ou seja, 6)> 5, portanto, 3, 5, 3 (em cm) podem ser os comprimentos dos lados de um triângulo.
(ii) Como 4 + 3 (isto é, 7) <8, portanto 4, 3, 8 (em cm) não podem ser os comprimentos dos lados de um triângulo.
Iii. Propriedades dos ângulos externos e ângulos opostos de um triângulo:
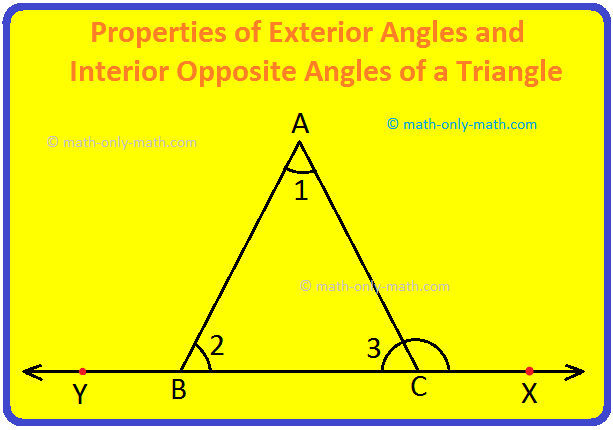
Considere um triângulo ABC. Produza seu lado BC a X.
Porte é chamado de ângulo externo de ∆ABC em C.
Da mesma forma, produzir CB lateral a y, então porte é um ângulo externo de ∆ABC em B.
Agora, porte isto, isto ângulo adjacente inside para eroCX em C, enquanto porte grafo e ero são chamados Inside ângulos opostos para eroCX em C.
Da mesma forma, porte isto, isto é, 2 é chamado de ângulo adjacente inside para ero e ero, BAC é o inside ângulos opostos para porte.
Vamos encontrar uma relação entre o ângulo externo e seus ângulos opostos interiores de um ∆ABC mostrado na figura acima.
Também em ∆ABC, ϩ1 + 2+ ♥3 = 180 graus; (Propriedade do ângulo Sum)
Assim, Exterior ACX = Soma de seus dois ângulos opostos interiores, onde ♥1 (= ângulo A) e quina (= ângulo B) são os dois ângulos interiores opostos do exterior ∠ACX
Da mesma forma, externo porte
ou seja, exterior porte = soma de seus dois ângulos interiores opostos
Agora, temos o seguinte:
1. Em um triângulo, um ângulo externo é igual à soma de seus dois ângulos opostos interiores.
2. Em um triângulo, um ângulo externo é maior do que qualquer um dos dois ângulos opostos do inside.
Responder:
A soma de todos os ângulos de um triângulo é sempre 180 °. Você pode desenhar qualquer número de triângulos e medir seus ângulos. Você encontrará, a soma dos ângulos de cada triângulo é de 180 °.
Responder:
A soma dos comprimentos de dois lados de um triângulo é sempre maior que o terceiro lado.
Você pode desenhar qualquer número de triângulos e medir seus lados. Em cada caso, você encontrará, a soma dos comprimentos de dois lados do triângulo é sempre maior que o comprimento do terceiro lado.
Não encontrou o que você estava procurando? Ou quero saber mais informações sobreSomente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.
