Assine o nosso Canal do youtube Para os vídeos, atualizações e dicas mais recentes.
Linhas:
Duas linhas ou dois segmentos de linha que se cruzam e se encontram em um ponto são chamados linhas que se cruzam ou Segmentos de linha que se cruzam.
O ponto comum nas linhas ou segmentos de linha nos quais eles se encontram é chamado de ponto de interseção. Por exemplo, ( overline {ab} ) e ( overline {cd} ) se encontram no ponto P. Aqui, p é um ponto de interseção.
Lembre -se de que duas linhas retas ou segmentos de linha podem se encontrar apenas em um ponto e, portanto, eles podem ter apenas um ponto de interseção.
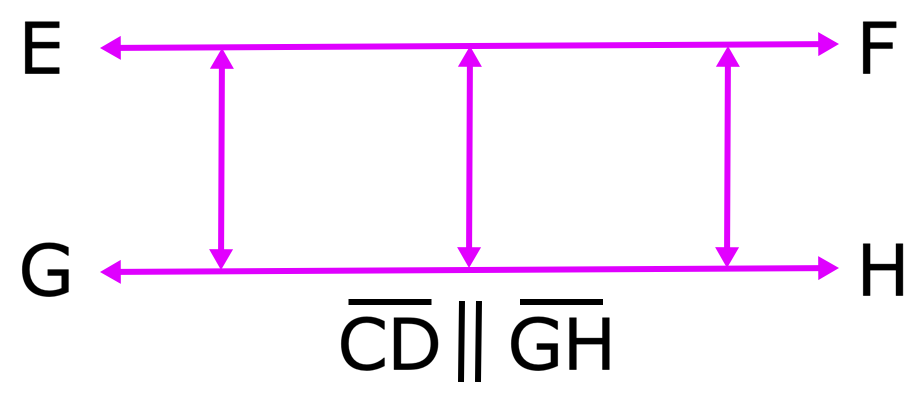
As linhas que nunca se encontram em nenhum momento são chamadas linhas paralelas. Tais linhas estão sempre a uma distância igual uma da outra. || é o símbolo para linhas paralelas. A distância entre duas linhas paralelas sempre será a mesma
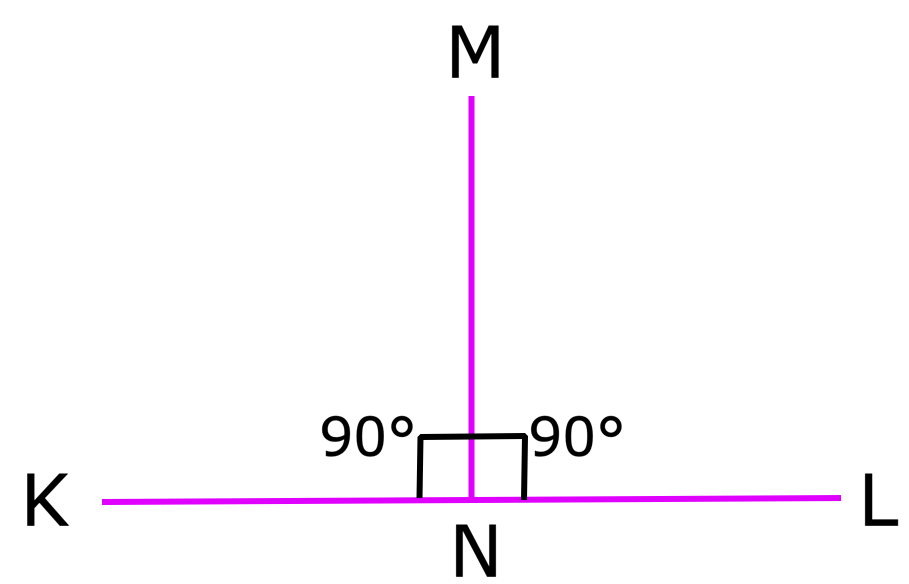
Quando duas linhas ou segmentos de linha se encontram em ângulo reto, eles são perpendiculares um ao outro. ⊥ é o símbolo para linhas perpendiculares.
( overline {mn} ) e ( overline {kl} ) são perpendiculares entre si.
Ângulos:
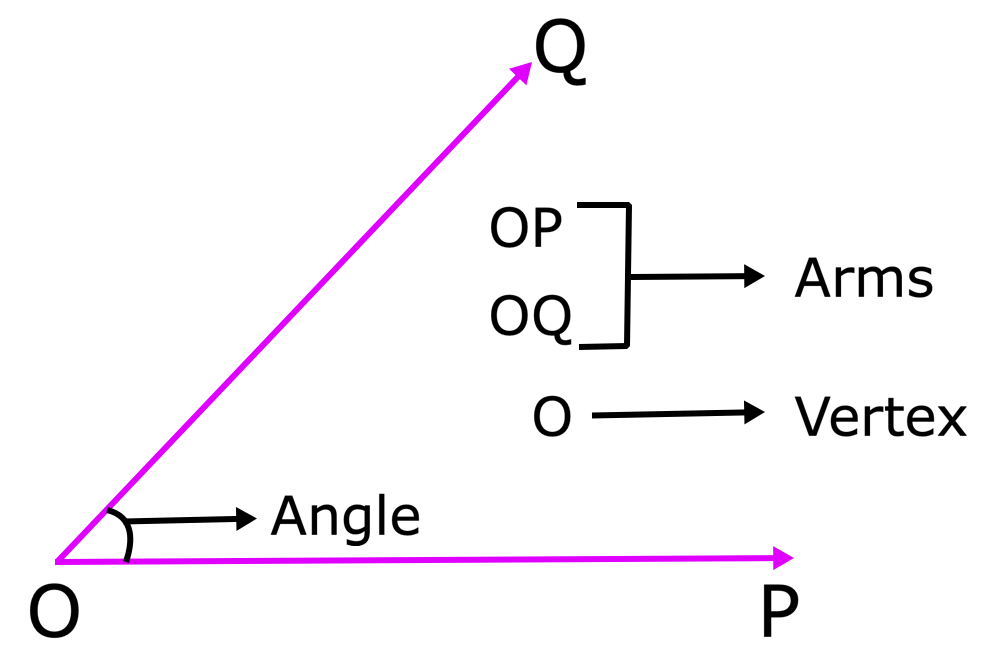
Dois raios começando de um ponto comum formam um ângulo. Os raios são chamados de braços do ângulo. O ponto comum é conhecido como o vértice do ângulo
Na figura, ( OverrightArrow {op} ) e ( OverrightArrow {oq} ) são os dois raios com um ponto remaining comum O. OP e OQ são os dois braços do ângulo e O é o vértice.
Lemos esse ângulo como eroPoq ou eroQOP, também o lemos como ero.
Um ângulo é medido em graus com a ajuda de um transferidor que geralmente é de forma semicircular.
Tipos de ângulos:
Já aprendemos sobre diferentes tipos de ângulos, como ângulo agudo, ângulo reto, and so forth.
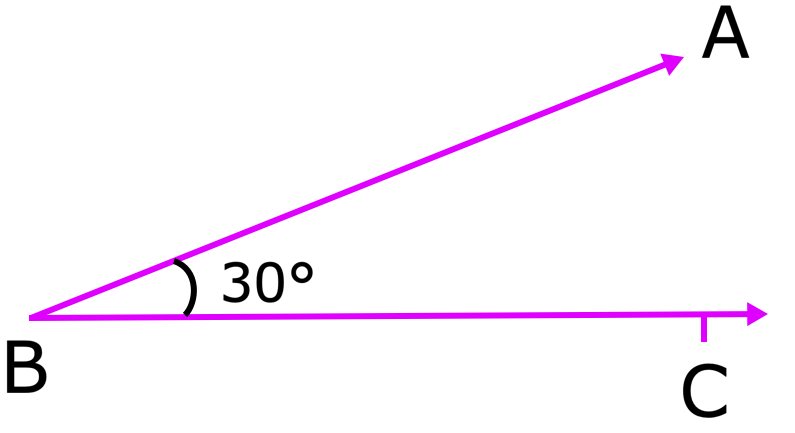
(i) ângulo agudo: Um ângulo menor que 90 ° é chamado de ângulo agudo. Na figura, o portebc é um ângulo agudo. ϨABC = 30 °
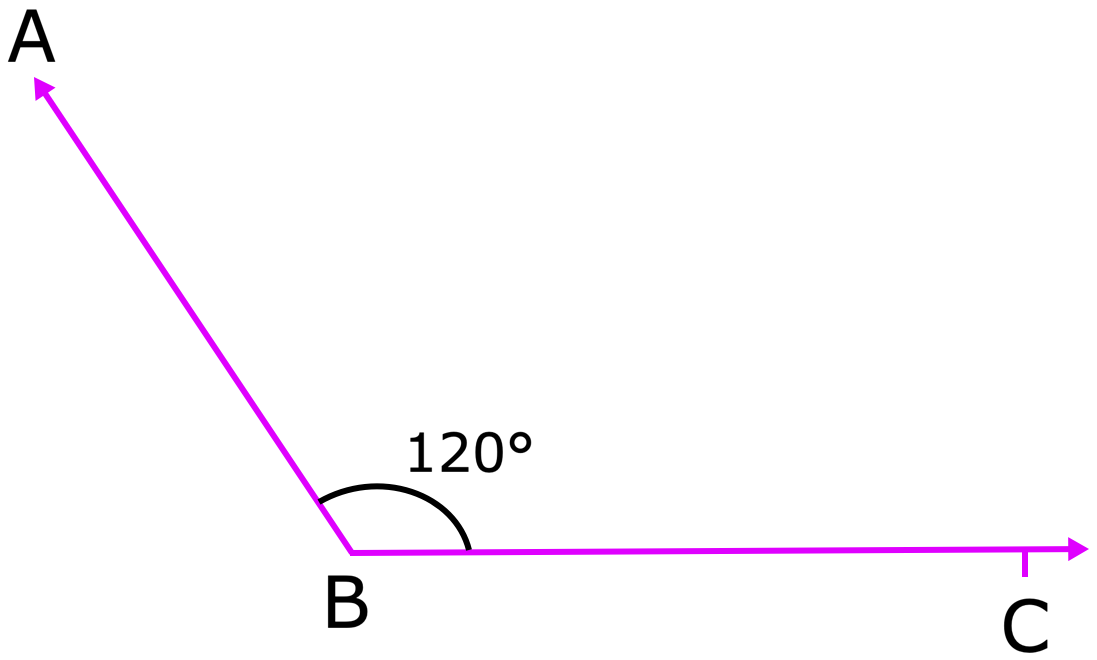
(ii) ângulo obtuso: Um ângulo maior que 90 °, mas menos de 180 graus é chamado de ângulo obtuso. Na figura, o ABC é um ângulo obtuso. ABABC = 120 °
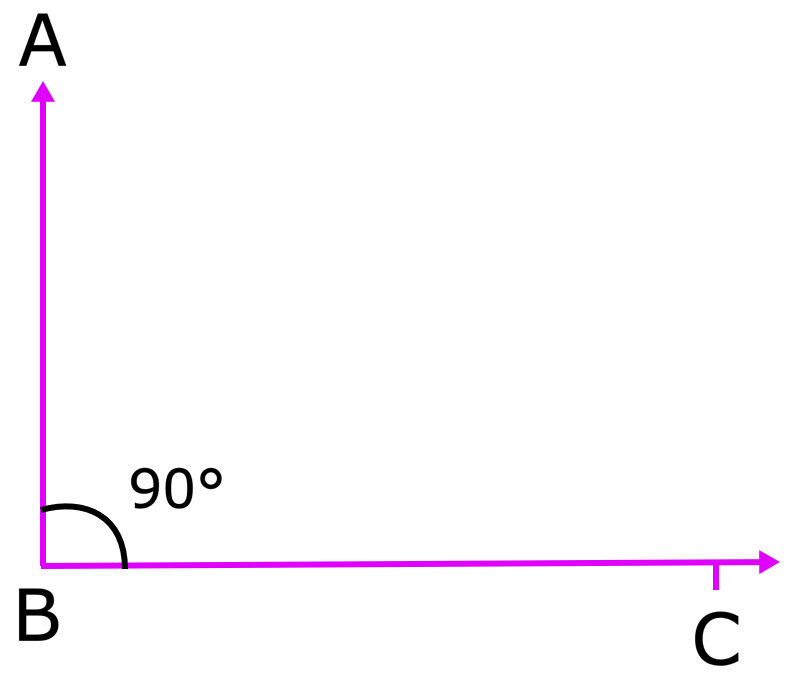
(iii) ângulo reto: Um ângulo que é 90 ° é chamado de ângulo reto. Na figura, o portebc é um ângulo reto. ABC = 90 °.
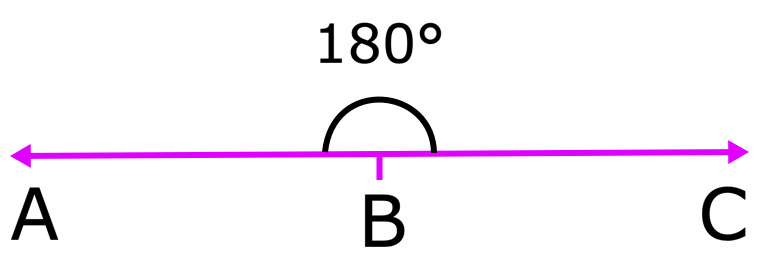
(iv) ângulo reto: Um ângulo que mede 180 ° é chamado de ângulo reto. Na figura, o ABC é um porte direto de 180 °.
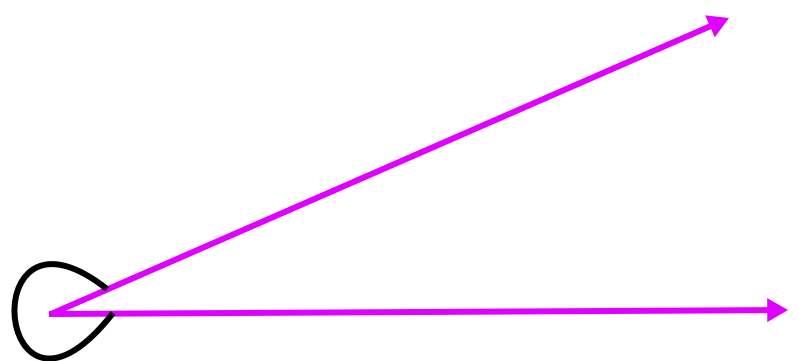
(v) ângulo reflexo: Um ângulo maior que 180 °, mas menor que 360 ° é chamado de ângulo reflexo.
(vi) ângulo inteiro: Um ângulo que é 360 ° é chamado de ângulo inteiro.
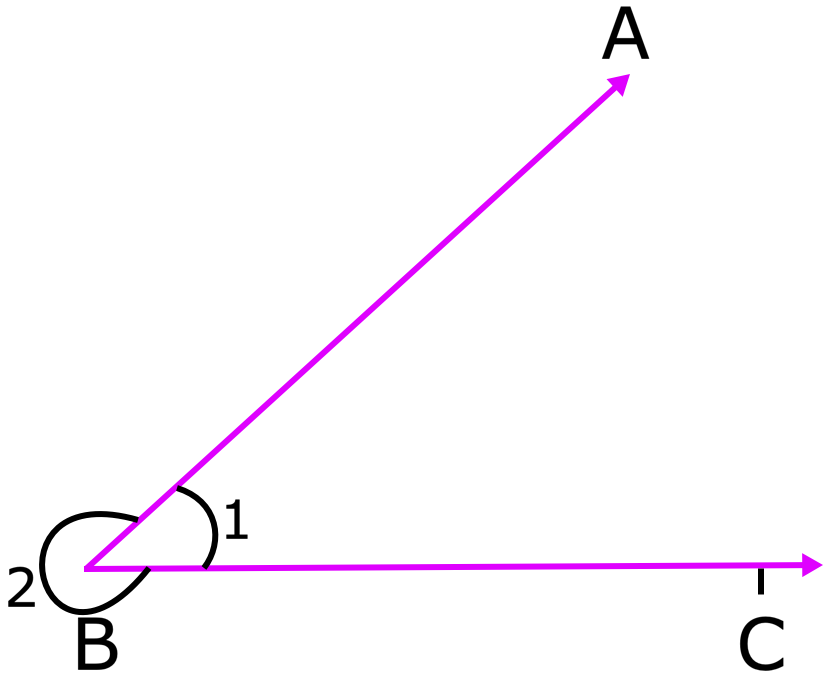
(vii) Inside e exterior de um ângulo: Sempre que dois raios ou dois segmentos de linha se reúnem em um ponto comum, eles formam dois ângulos
(a) Inside do ângulo, isto
(b) Exterior do ângulo, isto
Ângulos adjacentes, suplementares e complementares:
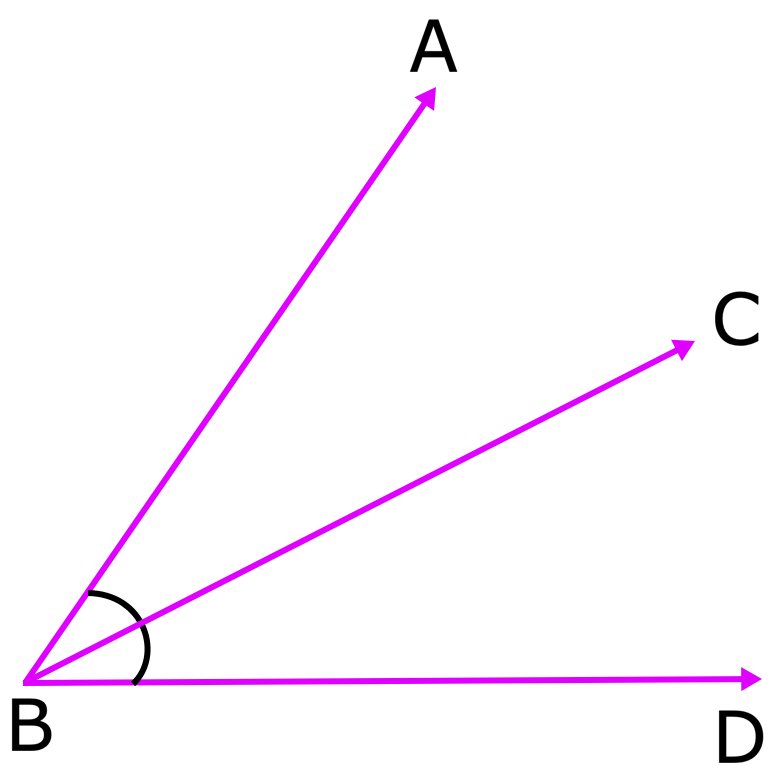
(viii) ângulos adjacentes:
Ângulos adjacentes ângulos que são lado a lado com um braço comum e vértice são chamados ângulos adjacentes. Aqui, eroBC e ero são ângulos adjacentes.
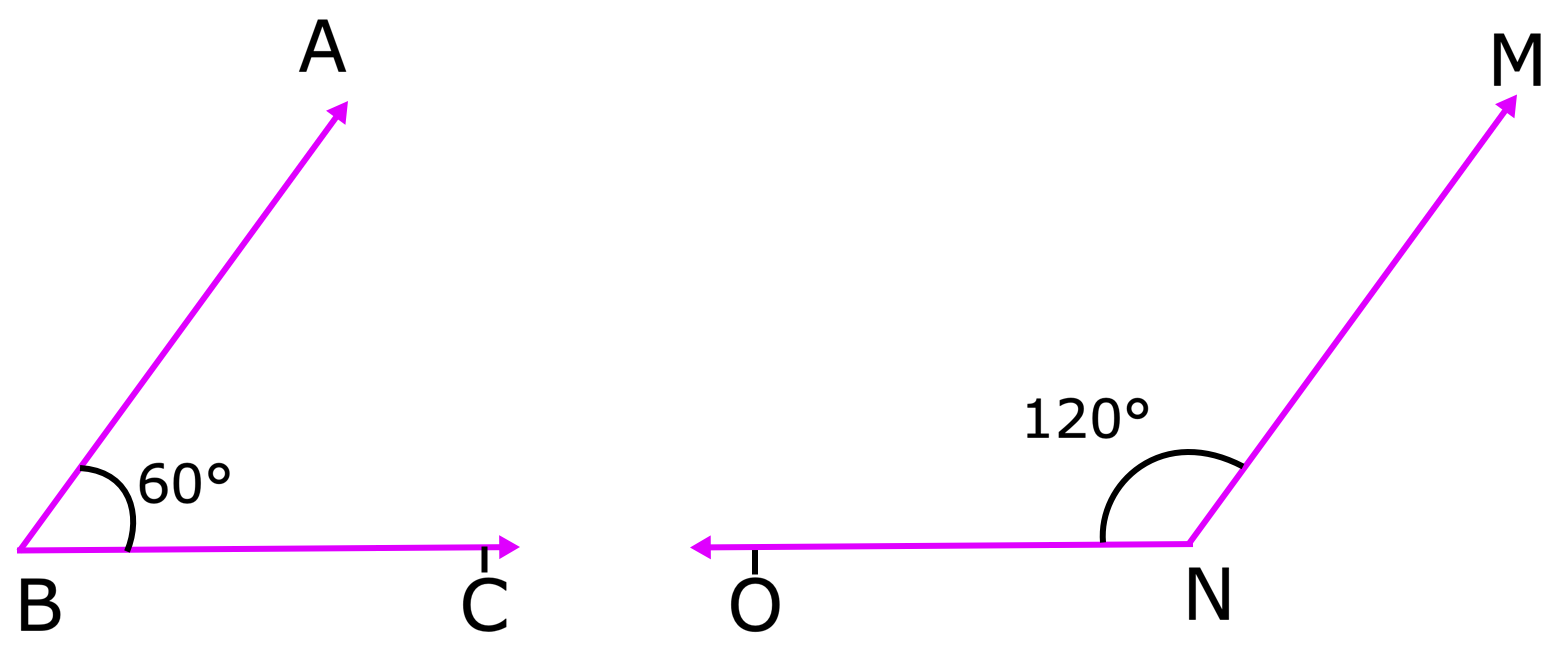
(ix) ângulos suplementares: Dois ângulos, cuja soma é 180 ° são chamados suplementar.
ABABC + porteMnO = 60 ° + 120 ° = 180 °
Portanto, porte porte e porte são ângulos suplementares. Cada um é chamado de suplemento ao outro.
Se a soma de dois ângulos adjacentes for de 180 °, eles são ângulos suplementares também.
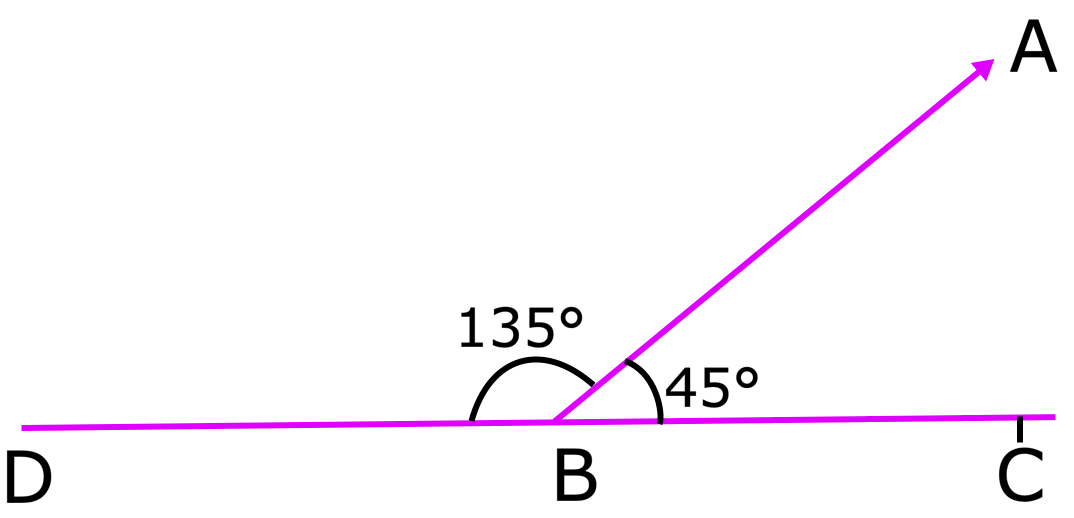
ABABC + porteBd = 45 ° + 135 ° = 180 °
Então, porte ∠ABC e ero, que são ângulos adjacentes, são ângulos suplementares também.
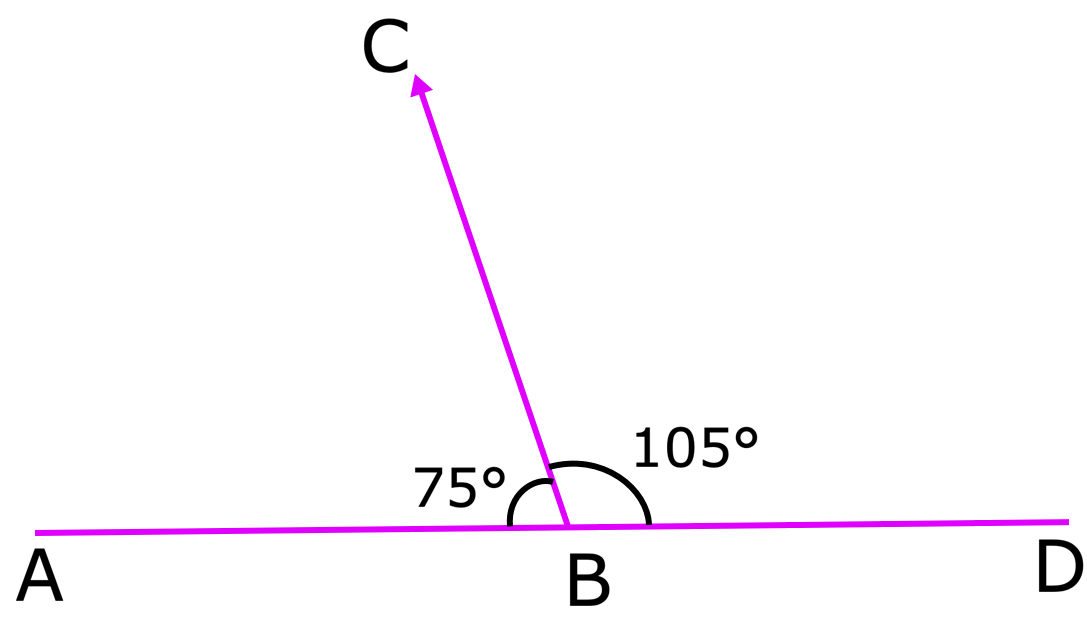
ABABC + portecbd = 75 ° + 105 ° = 180 °
Portanto, porte ∠ABC e ϩCBD, que são ângulos adjacentes, também são ângulos suplementares.
(x) ângulos complementares: Os ângulos cuja soma é 90 ° são chamados ângulos complementares. Nesse caso, cada ângulo é o complemento do outro ângulo.
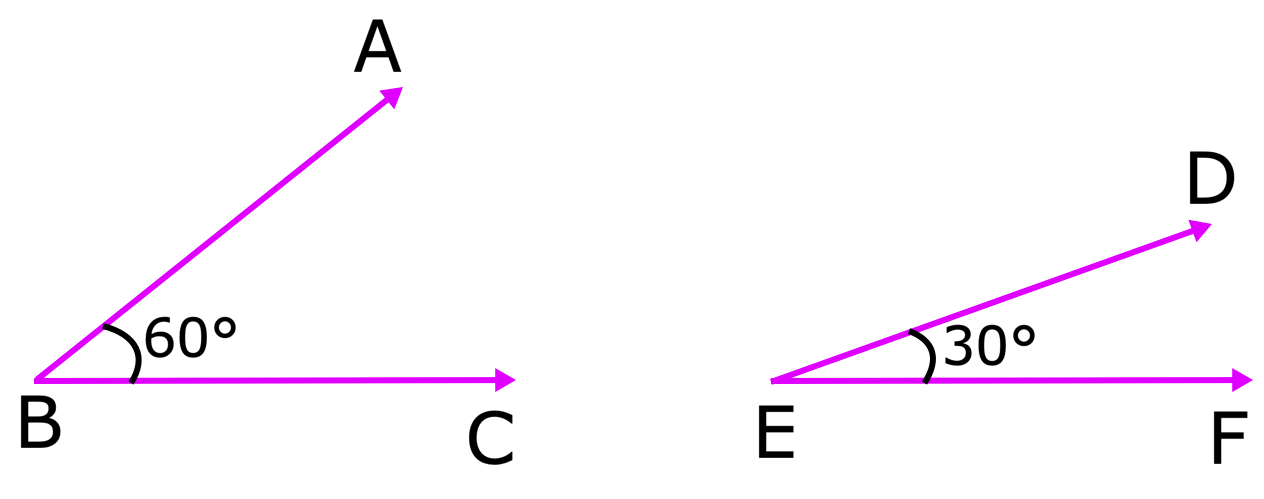
EroBC + porteDef = 60 ° + 30 ° = 90 °
Portanto, ϩABC e DEF são ângulos complementares.
Dois ângulos adjacentes cuja soma é 90 graus também são ângulos complementares.
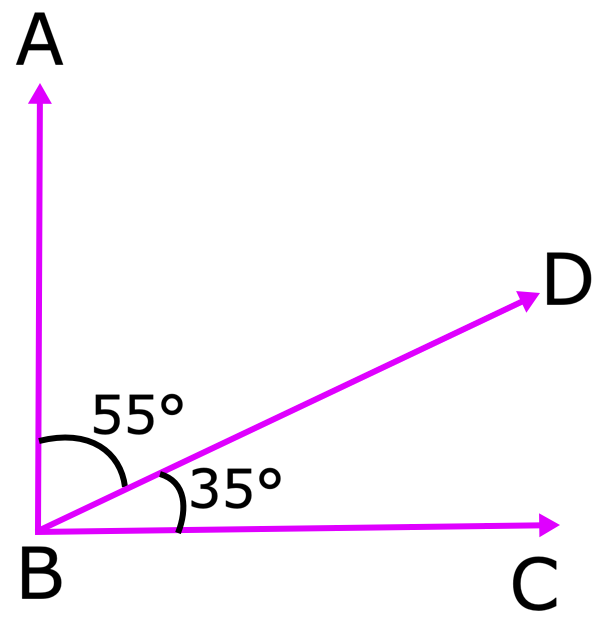
EroBd + portedbc = 55 ° + 35 ° = 90 °
Portanto, porte e porte também são ângulos complementares.
Planilha em linhas e ângulos
I. Preencha os espaços em branco.
(i) Um raio tem __________ ponto remaining.
(ii) Uma linha possui __________ pontos finais.
(iii) Os dois raios com um ponto comum formam um __________.
(iv) Um segmento de linha possui __________ pontos finais.
(v) Um ângulo menor que um ângulo reto é um ângulo __________.
(vi) Um ângulo possui __________ vértice e __________ braços.
(vii) Um segmento de linha tem um comprimento __________.
(viii) Em 6,00, o lado minuto e a hora de um relógio formam um ângulo de __________.
(ix) Um ângulo, maior que 180 °, mas menor que 360 ° é chamado de ângulo de __________.
(x) Um ângulo igual a 360 ° é chamado de ângulo de __________.
(xi) A soma de dois ângulos complementares é __________ °.
(xii) Os ângulos com um vértice comum e um braço comum são chamados ângulos __________.
(xiii) A soma de dois ângulos suplementares é sempre __________ °.
Responder:
EU. (i) um
(ii) Não
(iii) ângulo
(iv) Dois
(v) agudo
(vi) um; dois
(vii) definitivo
(viii) reto
(ix) Reflex
(x) inteiro
(xi) 180
(xii) adjacente
(xiii) 360
Problemas de matemática da 5ª série
De linhas e ângulos à página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.