Assine o nosso Canal do youtubePara os vídeos, atualizações e dicas mais recentes.
A geometria é um dos ramos mais antigos e principais da matemática. A medição da Terra é o significado exato da palavra ‘geometria’. A geometria começou quando os homens sentiram a necessidade de medir suas terras enquanto compravam e vendiam. Várias formas e figuras com as quais lidamos em geometria são chamados de figuras geométricas. Na geometria da 5ª série, aprendemos sobre a construção de figuras geométricas e estudamos suas propriedades básicas. Assim, pode -se dizer que a geometria é a ciência das propriedades e relações de figuras.
Aprenderemos sobre alguns conceitos e termos básicos em geometria.
Em termos de geometria, como ponto, linha e plano formam a base da geometria. Estes termos apontam, a linha e o plano não podem ser definidos com precisão. No entanto, damos exemplos para ilustrar o significado desses termos. A geometria tem tudo a ver com descrever formas e suas propriedades.
Já aprendemos sobre pontos, segmentos de linha, raios, linhas retas, ângulos and many others. Portanto, revisaremos esses termos em breve.
A geometria é uma ciência na qual estudamos algumas propriedades e relações de pontos, linhas, aviões e sólidos no espaço.
Vamos lembrar e revisar alguns dos conceitos que desenvolvemos anteriormente.
Ponto, linha, segmento de linha, raio e linha reta:
Apontar: Um círculo de raio zero é conhecido como ponto. O ponto é simplesmente um ponto (.) Um ponto não tem comprimento, sem largura ou altura (espessura).
Um ponto é representado por um ponto (.)
Os pontos são nomeados com letras maiúsculas A, B, C, D, and many others.
Pontos colineares: Os pontos que estão na mesma linha reta são chamados de pontos colineares. Os pontos A, B, C, D, E são pontos colineares porque todos eles estão deitados na mesma linha reta.
Pontos não colineares: Os pontos que não estão na mesma linha reta são chamados de não Pontos colineares. Os pontos A, B, C e D são pontos não colineares, porque todos eles não estão na mesma linha reta.
Linha: Os pontos se juntam para formar uma linha.
Uma linha não tem pontos finais.
Dada abaixo está a linha Mn.
Uma linha representada por dois pontos nela.
Linha Mn = ( OverleftRightarrow {mn} )
As duas setas mostram que se estende indefinidamente às duas direções.
Segmento de linha:
Um segmento de linha faz parte de uma linha.
Tem dois pontos finais.
A figura dada mostra um segmento de linha AB. Possui dois pontos finais A e B. Todo segmento de linha tem uma medida definitiva igual ao seu comprimento.
Um segmento de linha é representado com os dois pontos finais.
Segmento de linha AB = AB
Raio:
Um raio tem um ponto remaining de um lado e se estende indefinidamente do outro lado. Abaixo está um raio st.
Um raio é representado pelo ponto remaining e outro ponto nele.
A figura dada mostra Ray AB. O símbolo do raio AB é ( OverrightRow {ab} ). Tem um ponto remaining. Pode ser estendido a qualquer comprimento na direção de B de A.
Linha reta: A figura dada mostra uma linha reta AB. O símbolo da linha reta AB é ( overleftRightarrow {ab} ). Não tem pontos finais.
Avião: Um avião é uma superfície plana. Um avião se estende em todas as quatro direções infinitamente infinitamente em comprimento e largura.
Um avião não pode ser desenhado em um pedaço de papel. Não tem limite e o que desenhamos em um papel faz parte de um avião apenas, mas não o próprio avião. High de mesa, parede, teto da sala and many others. são os exemplos da parte do avião.
Em suma, um avião é uma superfície plana, como um topo de mesa, um livro and many others. O avião pode ser estendido em todas as direções. Portanto, uma parte do avião só pode ser representada em uma folha de papel. Pontos e linhas estão em um avião. É nomeado marcando três pontos nele.
Portanto, formas planas como linhas; Círculos e triângulos que podem ser desenhados em uma superfície plana, por exemplo, em um pedaço de papel são chamados de geometria plana.
Os objetos tridimensionais, como cubos, cubóides, prismas, cilindros e pirâmides, são chamados de geometria sólida.
Perguntas e respostas sobre geometria:
I. Quantos segmentos de linha são necessários para desenhar:
(i) Um retângulo
(ii) um quadrado
(iii) um cubo
(iv) Um triângulo
Respostas:
EU. (i) 4
(ii) 4
(iii) 12
(iv) 3
Responder: Um ponto mostra uma posição definitiva. Não tem comprimento, largura ou espessura. Não tem forma e tamanho. É representado por um ponto (.) E nomeado por uma letra maiúscula como A, B, C, P, Q, R, and many others.
Lembre -se, pontos que estão em linha reta são chamados Pontos colineares. Aqueles que não estão na mesma linha reta são chamados pontos não colineares.
2. O que é uma linha em matemática?
Responder:
Uma linha não tem comprimento fixo e pontos finais. Uma linha pode ser estendida indefinidamente em qualquer direção. Representamos uma linha como ( overleftRightarrow {xy} ).
3. O que é um segmento de linha em matemática?
Responder:
Uma parte de uma linha é conhecida como segmento de linha. Se ingressarmos em dois pontos P e Q, que estão em uma linha, obtemos um segmento de linha PQ. Os pontos P e Q são os pontos finais do segmento de linha. Tem um comprimento definitivo. Podemos representá -lo como ( overline {pq} ).
3. O que é um raio em matemática?
Responder:
Um raio faz parte de uma linha que tem um ponto de partida definitivo, mas vai indefinidamente em outra direção. É representado por AB. A é o seu ponto de partida.
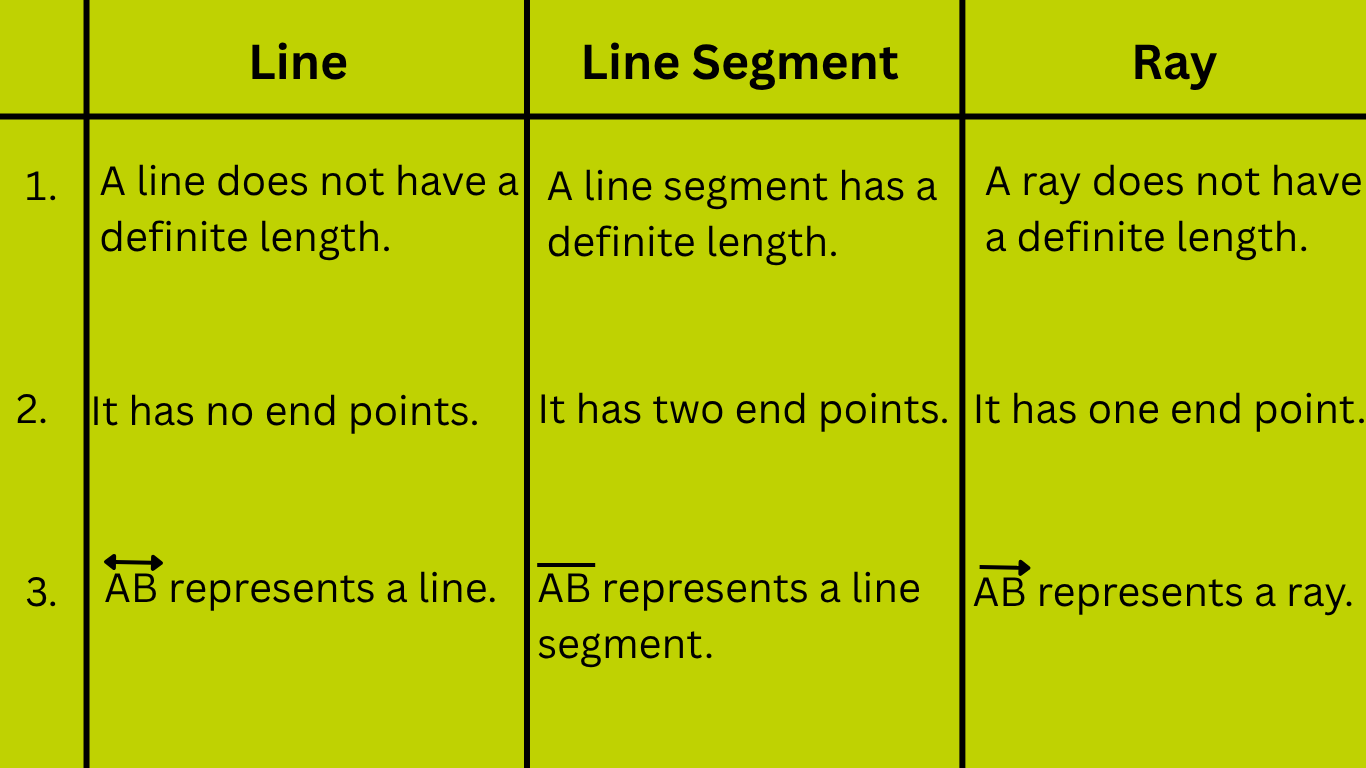
4. Qual é a diferença entre linha, segmento de linha e raio?
Não encontrou o que você estava procurando? Ou quero saber mais informações sobreSomente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.
