Em um quadrado mágico, todas as linhas, coluna e cada uma das diagonais somam o mesmo whole.
Aqui está uma praça mágica. Os números 1 a 9 são colocados nos quadrados pequenos de tal maneira que nenhum número é repetido e a soma dos três dígitos em termos de coluna, em termos de linha e na diagonal é igual a 15.
Este é um quadrado mágico de 3 por 3.
UM. Este é um quadrado mágico.
Todas as 3 linhas somam até 15.
Todas as 3 colunas somam até 15.
As 2 diagonais somam até 15.
Existem 8 linhas, cada uma totalizando 15.
Neste quadrado mágico, são usados números de 1 a 9. Em uma dessas linhas, os números aumentam em 1.
A diagonal é 4, 5, 6.
Olhe com cuidado e encontre em qual linha os números aumentam em (a) 2 (b) 3
Quadrados mágicos semelhantes também são feitos.

Magic Sq. (3 × 3) soma = 15 vídeo
https://www.youtube.com/watch?v=5hifemdmng4
Existem os exemplos de quadrados mágicos formados pelos números 5, 6, 7, 8, 9, 10, 11, 12 e 13, com a soma diagonalmente, em remar e coluna de 27


No mesmo padrão, outros quadrados mágicos podem ser formados.
(i) Os números são 2, 3, 4, 5, 6, 7, 8, 9 e 10, soma = 18
(ii) Os números são de 3 a 11 e soma = 21
(iii) Os números são de 4 a 12 e soma = 24
(iv) Os números são de 6 a 14 e soma = 30
(v) Os números são 7 a 15 e soma = 33
(vi) Os números são de 8 a 16 e soma = 36
(vii) Os números são 9 a 17 e soma = 39
Os quadrados mágicos com 4 ou mais linhas e colunas podem ser feitas.
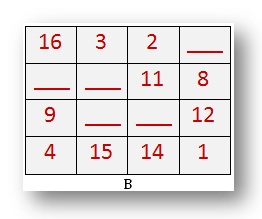
B. Este é um quadrado mágico de 4 por 4. Descubra os números ausentes. O que cada linha se aplica?
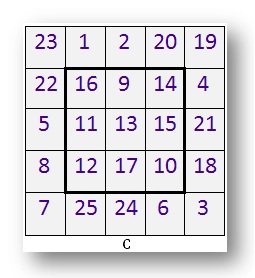
C. Este é um quadrado mágico de 5 por 5.
Possui 5 linhas e 5 colunas.
Descubra o whole da linha.
Verifique se cada uma das 5 linhas, 5 colunas e 2 diagonais somam o mesmo número.
No centro deste quadrado mágico de 5 por 5, há um quadrado de 3 por 3. Desenhe este 3 por 3 quadrado em uma folha de papel.
Copie o número em cada caixa.
Isso é 3 por 3 quadrados UM um quadrado mágico?
Qual é a linha whole de cada linha e coluna?
Qual é o whole das duas diagonais? Os números aumentam em 1 em alguma das linhas? Colorir essa linha.
Use cores diferentes nas linhas de sombra, onde os números aumentam em (a) 2 (b) 3.
D. Este é um quadrado mágico de 6 por 6.
Encontre o whole da linha.
Verifique se algumas das linhas e colunas somam esse número.
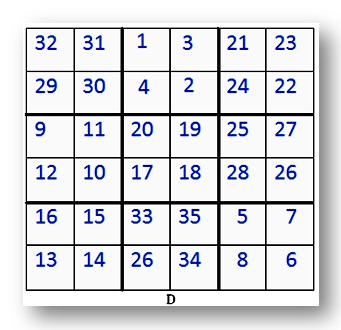
Observe que as linhas grossas dividem o quadrado em 9 quadrados menores.
Cada pequeno quadrado tem 4 números.
O que você percebe sobre os 4 números em cada um desses pequenos quadrados?
Adicione os 4 números em cada um dos 9 quadrados.
Escreva sua resposta em um quadrado de 3 por 3.
Os dois primeiros quadrados foram feitos para você.
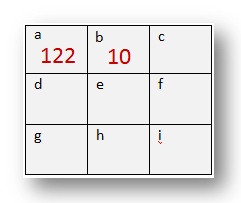
(a) 29 + 30 + 31 + 32 = 122
(b) 1 + 2 + 3 + 4 = 10
(c) 21 + 22 +23 + 24 = ____
(d) 9 + 10 + 11 + 12 = ____
(e) 17 + 18 + 19 + 20 = ____
(f) 25 + 26 + 27 + 28 = ____
(g) 13 + 14 + 15 + 16 = ____
(h) 33 + 34 + 35 + 26 = ____
(i) 5 + 6 + 7 + 8 = ____
Agora adicione os números em cada linha, coluna, diagonal e confirme que isso também é um quadrado mágico!
Observe o padrão de número
1 ∙ 1 ∙ 2 ∙ 3 ∙ 5 ∙ 8 ∙ 13 ∙ 21 ∙ 34
Cada número após o segundo número é igual à soma dos dois números anteriores.
Este tipo de relacionamento é chamado de Sequência de Fibonacci. Foi desenvolvido por Leonardo Fibonacci, da Itália, por volta do ano 1200.
Podemos observar números da sequência de Fibonacci em vários lugares da natureza; pétalas de flores; folhas de plantas; Escalas de abacaxi e nós de uma pinha.
Observe o padrão de número
1 ∙ 3 ∙ 6 ∙ 10 ∙ 15 ∙ 21 21
Esta sequência de números é composta de Número triangular.
A sequência começa com 1. Então
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
15 + 6 = 21
Há outro fato interessante.
Você pode tomar um número de 3 dígitos como 356.
Se escrevermos depois do mesmo número de três dígitos, obtemos 356356.
Este número é dividido por 7, 11 e 13.
479479 também é dividido por 7, 11 e 13.
Da mesma forma, outros números podem ser feitos que seriam divisíveis em 7, 11 e 13.
Conceito relacionado
● Padrões e matemática psychological
● Contando números em padrão adequado
● Número formado por qualquer poder
● Padrões
Atividades matemáticas da 4ª série
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.







