Conversão de frações em decimais | Exemplos resolvidos

Ao converter frações em decimais, sabemos que os decimais são frações com denominadores 10, 100, 1000 and many others. Para converter outras frações em decimais, seguimos as seguintes etapas:

Passo I: Converta a fração em uma fração equivalente com o denominador 10 ou 100 ou 1000, se não for assim.

Etapa II: Pegue o numerador da fração dada. Em seguida, marque o ponto decimal após um lugar ou dois lugares ou três lugares da direita para a esquerda, se o denominador da fração fornecida for de 10 ou 100 ou 1000, respectivamente.

Observe que; Insira os zeros à esquerda do numerador se o numerador tiver menos dígitos.

● Para converter uma fração com 10 no denominador, colocamos o ponto decimal em um lugar esquerdo do primeiro dígito no numerador.

Por exemplo:

(i) ( frac {6} {10} ) = .6 ou 0.6

(ii) ( frac {16} {10} ) = 1.6

(iii) ( frac {116} {10} ) = 11.6

(iv) ( frac {1116} {10} ) = 111.6

● Para converter uma fração com 100 no denominador, colocamos o ponto decimal dois lugares restantes do primeiro dígito no numerador.

Por exemplo:

(i) ( frac {7} {100} ) = 0,07

(ii) ( frac {77} {100} ) = 0,77

(iii) ( frac {777} {100} ) = 7,77

(iv) ( frac {7777} {100} ) = 77,77

● Para converter uma fração com 1000 no denominador, colocamos o ponto decimal três lugares restantes do primeiro dígito no numerador.

Por exemplo:

(i) ( frac {9} {1000} ) = 0,009

(ii) ( frac {99} {1000} ) = 0,099

(iii) ( frac {999} {1000} ) = 0,999

(iv) ( frac {9999} {1000} ) = 9.999

O problema nos ajudará a entender como converter a fração em decimal.

Em ( frac {351} {100} ) Vamos mudar a fração para decimal.

Primeiro, escreva o numerador e depois divida o numerador por denominador e full a divisão.

Coloque o ponto decimal de modo que o número de dígitos na parte decimal seja o mesmo que o número de zeros no denominador.

Vamos verificar a divisão de decimal, mostrando uma divisão completa de passo decimal passo a passo.

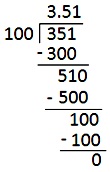
Sabemos que quando o número obtido dividindo -se pelo denominador é a forma decimal da fração.

Pode haver duas situações na conversão de frações em decimais:

• Quando a divisão pára após um certo número de etapas, pois o restante se torna zero.

• Quando a divisão continua, pois há um restante após cada etapa.

Aqui, discutiremos quando a divisão estiver concluída.

Explicação sobre o método usando um exemplo passo a passo:

• Divida o numerador por denominador e full a divisão.

• Se um restante diferente de zero for deixado, coloque o ponto decimal no dividendo e no quociente.

• Agora, coloque zero à direita do dividendo e à direita do restante.

• Divida como no caso de todo o número repetindo o processo acima até que o restante se torne zero.

1. Convert ( frac {233} {100} ) em decimal.

Solução:

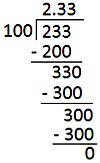
2. Expresse cada um dos seguintes como decimais.

(i) ( frac {15} {2} )

Solução:

( frac {15} {2} )

= ( frac {15 × 5} {2 × 5} )

= ( frac {75} {10} )

= 7,5

(Tornando o denominador 10 ou superior de 10)

(ii) ( frac {19} {25} )

Solução:

( frac {19} {25} )

= ( frac {19 × 4} {25 × 4} )

= ( frac {76} {100} )

= 0,76

(iii) ( frac {7} {50} )

Solução:

( frac {7} {50} ) = ( frac {7 × 2} {50 × 2} ) = ( frac {14} {100} ) = 0,14

Observação:

A conversão de frações em decimais quando o denominador não puder ser convertido em 10 ou mais poder de 10 será realizado na divisão de decimais.

Regras de trabalho para conversão de frações em decimais:

Para converter uma fração comum em número decimal, precisamos seguir as etapas a seguir.

Passo I: Altere a fração comum dada em uma fração equivalente cujo denominador é de 10, 100 ou 1000, and many others.

Etapa II: Conte o número de zeros no denominador após 1.

Etapa III: No numerador, comece da extrema direita e mova o ponto decimal para

Exemplos na conversão de frações em decimais:

1. Converta as seguintes frações em decimais.

(i) ( frac {3} {4} )

(ii) 5 ( frac {1} {2} )

(iii) ( frac {31} {125} )

Solução:

(i) ( frac {3} {4} ) = ( frac {3 × 25} {4 × 25} ) = ( frac {75} {100} ) = 0,75

(ii) 5 ( frac {1} {2} ) = ( frac {11} {2} ) = ( frac {11 × 5} {2 × 5} ) = ( frac {55} {10} )

(iii) ( frac {31} {125} ) = ( frac {31 × 8} {125 × 8} ) = ( frac {248} {1000} ) = 0,248

2. Converta 2 ( frac {7} {16} ) em um decimal.

Solução:

2 ( frac {7} {16} ) = ( frac {2 × 16 + 7} {16} ) = ( frac {32 + 7} {16} ) = ( frac {39} {16} )

Agora, ( frac {39} {16} ) = ( frac {39 × 625} {16 × 625} ) = ( frac {24375} {10000} ) = 2.4375

Assim, ( frac {39} {16} ) = 2.4375

3. Expresse as seguintes frações como decimais:

(eu) ( frac {3} {10} )

Solução:

Usando o método acima, temos

( frac {3} {10} )

= 0,3

(ii) ( frac {1479} {1000} )

Solução:

( frac {1479} {1000} )

= 1,479

(iii) 7 ( frac {1} {2} )

Solução:

7 ( frac {1} {2} )

= 7 + ( frac {1} {2} )

= 7 + ( frac {5 × 1} {5 × 2} )

= 7 + ( frac {5} {10} )

= 7 + 0,5

= 7,5

(4) 9 ( frac {1} {4} )

Solução:

9 ( frac {1} {4} )

= 9 + ( frac {1} {4} )

= 9 + ( frac {25 × 1} {25 × 4} )

= 9 + ( frac {25} {100} )

= 9 + 0,25

= 9.25

(v) 12 ( frac {1} {8} )

Solução:

12 ( frac {1} {8} )

= 12 + ( frac {1} {8} )

= 12 + ( frac {125 × 1} {125 × 8} )

= 12 + ( frac {125} {1000} )

= 12 + 0,125

= 12.125

Convertendo uma fração comum em uma fração decimal:

Para converter uma fração comum em uma fração decimal, seguimos o método da divisão. Neste método, tomamos essas etapas.

Regras de trabalho para converter uma fração comum em uma fração decimal:

Passo I: Divida os numeradores pelo denominador até que um restante diferente de zero seja obtido.

Etapa II: Coloque um ponto decimal no dividendo e no quociente.

Etapa III: Coloque um zero à direita do ponto decimal no dividendo e à direita do restante sempre que necessário.

Etapa IV: Divida novamente como fazemos em números inteiros.

Etapa V: Repita a etapa IV até que o restante seja zero.

Exemplos em Convertendo uma fração comum em uma fração decimal:

1. Converta em decimal.

(eu) ( frac {3} {4} )

(ii) 4 ( frac {1} {4} )

Solução:

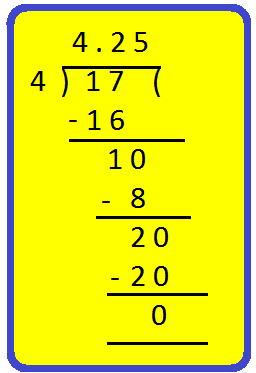
(i) Divida o numerador 3 pelo denominador 4.

Portanto, ( frac {3} {4} ) = 0,75

(ii) 4 ( frac {1} {4} )

Primeiro converter em fração inadequada

4 ( frac {1} {4} ) = ( frac {4 × 4 + 1} {4} ) = ( frac {17} {4} )

Agora, divida o numerador 17 pelo denominador 4.

Portanto, 4 ( frac {1} {4} ) = 4.25

Planilha sobre a conversão de frações em decimais:

1. Converta os seguintes números fracionários em números decimais:

(i) ( frac {7} {10} )

(ii) ( frac {23} {100} )

(iii) ( frac {172} {100} )

(iv) ( frac {4905} {100} )

(v) ( frac {9} {1000} )

(vi) ( frac {84} {1000} )

(i) ( frac {672} {1000} )

(i) ( frac {4747} {1000} )

Respostas:

(i) 0,7

(ii) 0,23

(iii) 1.72

(iv) 49.05

(v) 0,009

(vi) 0,084

(i) 0,672

(i) 4.747

2. Expresse as seguintes frações como números decimais:

(i) ( frac {2} {5} )

(ii) ( frac {9} {25} )

(iii) ( frac {8} {20} )

(iv) ( frac {22} {100} )

(v) 2 ( frac {3} {4} )

(vi) 9 ( frac {7} {25} )

(vii) ( frac {205} {125} )

(viii) 16 ( frac {16} {40} )

(ix) ( frac {5926} {1000} )

Responder:

2. (i) 0,4

(ii) 0,36

(iii) 0,4

(iv) 0,22

(v) 2,75

(vi) 9.36

(vii) 1.64

(viii) 16.4

(ix) 5.926

● Conceito relacionado

● Decimais

● Números decimais

● Frações decimais

● Como e diferente de decimais

● Comparando decimais

● Lugares decimais

● Conversão de decimais diferentes para decimais

● Expansão decimal e fracionária

● Terminando decimal

● Decimal não terminante

● Convertendo decimais em frações

● Conversão de frações em decimais

● HCF e LCM de decimais

● Repete ou recorrente decimal

● Decimal recorrente puro

● Decimal recorrente misto

● Regra de Bodmas

● Regras de Bodmas/Pemdas – envolvendo decimais

● Regras de Pemdas – envolvendo números inteiros

● Regras de Pemdas – envolvendo decimais

● Regra de Pemdas

● Regras de Bodmas – envolvendo números inteiros

● Conversão de decimal recorrente puro em fração vulgar

● Conversão de decimais recorrentes mistos em frações vulgares

● Simplificação de decimal

● Decimais arredondados

● Decimais arredondados para o número inteiro mais próximo

● Decimais arredondados para os décimos mais próximos

● Decimais arredondados para os centésimos mais próximos

● Ao redor de um decimal

● Adicionando decimais

● Subtraindo decimais

● Simplifique decimais envolvendo decimais de adição e subtração

● Multiplicando decimal por um número decimal

● Multiplicando decimal por um número inteiro

● Dividindo decimal por um número inteiro

● Dividindo decimal por um número decimal

Problemas de matemática da 7ª série

Da conversão de frações a decimais e página inicial