Na divisão por números de dois dígitos, praticaremos dividir dois, três, quatro e cinco dígitos por números de dois dígitos.
Considere os seguintes exemplos de divisão por números de dois dígitos:
Vamos usar nosso conhecimento da estimativa para encontrar o quociente actual.
1. Divida 94 por 12
Arredondar o número
94 ÷ 12 → 90 ÷ 10
Quociente estimado = 9
Para encontrar o quociente actual, multiplique o divisor 12 pelo quociente estimado.
12 × 9 = 108
12 × 8 = 96
12 × 7 = 84
108> 94
96> 94
O quociente actual, encontramos é 7.
Verificar:
Quociente – 7
Restante – 10
12 × 7 + 10 = 94

2. Divida 96 por 16
Solução:
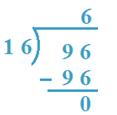
16 x 6 = 96, então, 6 será o quociente.
Pesquisamos o possível quociente. O divisor é um número de dois dígitos.
Então, 96 é tomado como dividendo.
Portanto, quociente = 6
Número de 2 dígitos por vídeo de divisão de 2 dígitos de 2 dígitos
https://www.youtube.com/watch?v=j39bi-0bpqg
Assine o nosso Canal do youtube Para os vídeos, atualizações e dicas mais recentes.
3. Divida 88 por 17
Solução:
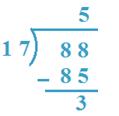
17 x 5 = 85 e 17 x 6 = 102,
85 <88 Mas 102> 88
Então, 5 será o quociente
Portanto, quociente = 5, restante = 3
Número de 3 dígitos por número de divisão de 2 dígitos de 2 dígitos
https://www.youtube.com/watch?v=rkaa3e9mfym
Assine o nosso Canal do youtube Para os vídeos, atualizações e dicas mais recentes.
4. Divida 192 por 24
Solução:
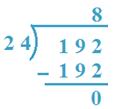
19 <24, então, 192 serão tomados como dividendos.
24 x 8 = 192. Então, 8 será o quociente.
Portanto, quociente = 8
5. 510 ÷ 32 ⟶ 500 ÷ 30 ⟶ 50 ÷ 3
Quociente estimado = 16
Tentar:
32 × 16 = 512
32 × 15 = 480
512> 510
O quociente actual é 15
6. Divida 275 por 24
Solução:
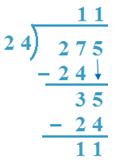
(a) 27> 24, 24 x 1 = 24, 24 x 2 = 48
Então, eu será quociente.
Aqui, 27 é 27T ou 270
Então, 1T ou 10 é o quociente.
(b) 275 -240 = 35, 24 x 1. = 24,
Então, 1 é o quociente.
24 x 11 + 11 = 264 + 11 = 275
Portanto, o resultado é verificado
Portanto, quociente = 11, restante = 11
7. Divida 803 por 70
Solução:
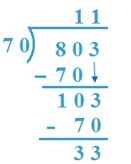
(a) 80> 70,
Então, 80T serão tomados como dividendos
70 x 1 = 70, 70 x 2 = 140
Então, 1T será quociente.
(b) 803 – 700 = 103, 70 x 1 = 70, 70 x 2 = 140
Então, eu será quociente.
70 x 11 + 33 = 770 + 33 = 803
Portanto, o resultado é verificado
Portanto, quociente = 11, restante = 33
8. Divida 345 por 49
Solução:
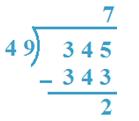
34 <49, então, 345 serão tomados como dividendos.
Pelo julgamento 49 x 7 = 343, que fica perto de 345
Então, 7 serão quocientes.
Verificação: 49 x 7 + 2 = 343 + 2 = 345
Portanto, quociente = 7, restante = 2
9. Divida 1432 por 28.
Solução:
|
EU: 1 <28 14 <28 Portanto, pegue 143 Ii: Temos 28 × 6 = 168; 28 × 5 = 140 Desde 140 <143, escreva 5 como primeiro dígito do quociente. Escreva o produto 26 × 5 = 140 abaixo de 143 e subtraia. Iii: 143 – 140 = 3; Derrubar 2 32> 28 Temos 28 × 1 = 28 <32. 28 × 2 = 56> 32 Desde 28 <32, escreva 1 como o segundo dígito do quociente. Escreva o produto 28 × 1 = 28 abaixo e subtraia. 4: 32 – 28 = 4 Desde 4 <28, pare a divisão. |
10. Divida 4963 por 14
Solução:
(I Método)
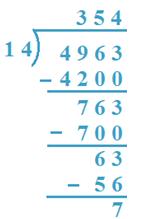
(a) 14 x 3 = 42 e 14 x 4 = 56, 42 <49 e 56> 49
Então, 3H será quociente.
(b) 4963 – 4200 = 763, 14 x 5 = 70 e 14 x 6 = 84
Então, 5T será quociente.
(c) 763 – 700 = 63, 14 x 4 = 56, 14 x 5 = 70
56 <63, 70> 63
Portanto, 4 é o quociente.
Verificação: 14 x 354 + 7 = 4956 + 7 = 4963
Portanto, quociente = 354, restante = 7
(II Método)
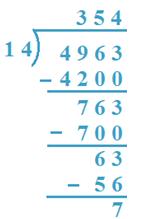
(a) 14 x 3 = 42, 14 x 4 = 56,
Portanto, 3H será quociente.
49 – 42 = 7, 6 é transportado
(b) 14 x 5 = 70, 14 x 6 = 84,
Portanto, 5T será quociente.
76 – 70 = 6, 3 é carregado.
14 x 4 = 56, 14 x 5 = 70,
Portanto, 4 será quociente.
63 – 56 = 7 é o restante
Quociente = 354
Restante = 7
Verificação:
Quociente x divisor + restante
= 354 x 14 + 7
= 4956 +7
= 4963 (dividendo)
Então, o resultado é verificado
11. Divida 47320 por 35
Solução:
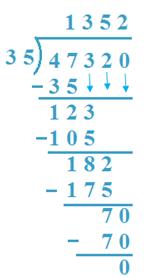
(a) 47 é dividido por 35, 35 x 1 = 35 <47,
35 x 2 = 70> 47, então, 1 th é quociente.
47 – 35 = 12, 3 é transportado
(b) 123h é dividido por 35, 35 x 3 = 105 <123
35 x 4 = 140> 123, então, 3 h é quociente
123 – 105 = 18, 2 é carregado.
(c) 182 t é dividido por 35, 35 x 5 = 175 <182
35 x 6 = 210> 182, portanto, 5T é quociente.
182 – 175 = 7, 0 é carregado.
(d) 70 é dividido por 35, 35 x 2 = 70,
2 é o quociente
70 – 70 = 0
Verificação: 35 x 1352 + 0 = 47320.
Tão verificado.
Portanto, quociente = 1352 restante = 0
12. Divida 50360 por 43
Solução:
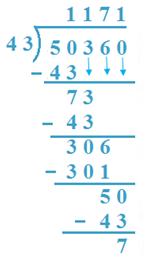
(a) 50º é dividido por 43, 43 x 1 = 43 <50.
Então, 1 th é quociente, 50 – 43 = 7,3 é retirado.
(b) 73 h é dividido por 43, 43 x 1 = 43 <73
43 x 2 = 86> 73.
Então, 1H é o quociente, 73 – 43 = 30, 6 é retirado.
(c) 306 t é dividido por 43, 43 x 7 = 301 <306
7 t é quociente, 306 – 301 = 5, 0 é retirado
(d) 50 é dividido por 43, 1 é quociente
50 – 43 = 7 é o restante
Verificação: 1171 x 43 + 7 = 50353 + 7 = 50360.
Resultado é verificado.
Quociente = 1171 restante = 7
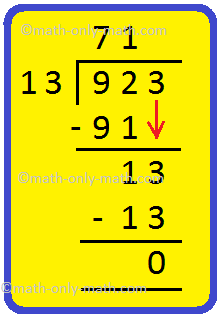
13. Divida 923 por 13
Solução:
|
Vamos dividir 923 por 13. Passo I: Como o divisor é um número de 2 dígitos, consideramos 92 o número de 2 dígitos à esquerda extrema do dividendo. 92> 13, sabemos que 13 x 7 = 91 Escrevemos 7 no quociente. Subtrair 91 de 92. Etapa II: Abaixe 3 e escreva no lado direito do restante. 13 é o novo dividendo. Etapa III: Divida 13 por 13. Sabemos 13 x 1 = 13. Escreva 1 no quociente. Subtrair 13 de 13. O restante é 0. |
Portanto, quociente = 71 e restante = 0. |
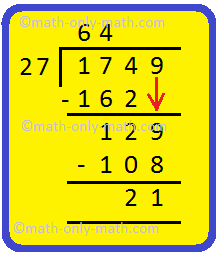
14. Divida 1749 por 27 e verifique sua resposta.
|
Solução: Vamos dividir 1749 por 27. Passo I: O divisor 27 é maior que o número de 2 dígitos à esquerda extrema do dividendo. Portanto, pegamos o número de 3 dígitos que é 174 e dividimos por 27. Escreva 6 no quociente e subtraia 162 de 174. Etapa II: Abaixe 9 e escreva no lado direito do restante. 129 é o novo dividendo. Etapa III: Divida 129 por 27. Escreva 4 no quociente e subtraia 108 de 129. O restante é 21 |
Portanto, quociente = 64 e restante = 21 |
Verificação:
Nós sabemos disso
Dividendo = quociente x divisor + restante
= 64 x 27 + 21
= 1728 + 21
= 1749
1749 é o dividendo, conforme dado na questão.
15. Divida 15642 por 32
Solução:
|
EU: 1 <32 15 <32 Portanto, pegue 156 Ii: Temos 32 × 5 = 160> 156 32 × 4 = 128 <156 Desde 128 <156, escreva 4 como primeiro dígito do quociente. Escreva o produto 32 × 4 = 128 abaixo de 156 e subtraia. Iii: 156 – 128 = 28. Abaixe 4. 284> 32. Temos 32 × 9 = 288> 284. 32 × 8 = 256 <284. Desde 256 <284, escreva 8 como o segundo dígito do quociente. Escreva o produto 32 × 8 = 256 abaixo de 284 e subtraia. 4: 284 – 256 = 28. Abaixe 2. 282> 32. Temos 32 × 9 = 288> 282 32 × 8 = 256 <282. V: Escreva 8 como o terceiro dígito do quociente. Escreva o produto 32 × 8 = 256 abaixo de 282 e subtraia. 282 – 256 = 26. Desde 26 <32, pare a divisão. |
Atividade de divisão
Objetivo: Dividindo um número de 2 dígitos por 9 usando o método de atalho.
Materiais necessários: Pen e papel apenas.
Procedimento/demonstração: Podemos dividir qualquer número de 2 dígitos em 9 rapidamente.
Tipo 1: Quando a soma dos dígitos é menor que 9.
Nesse caso, o dígito das dezenas do dividendo fornece quociente e a soma dos dois dígitos dá o restante.
Tipo 2: Quando a soma dos dígitos é maior ou igual a 9, mas menor que 18. Nesse caso, 1 a mais que o dígito das dezenas do dividendo dá o quociente. Para obter o restante, subtraia 9 da soma dos dígitos do dividendo.
75 ÷ 9 fornece quociente = 7 + 1 = 8 e restante = 12 – 9 = 3
63 ÷ 9 fornece quociente = 6 + 1 = 7 e restante = 9 – 9 = 0
Planilha sobre divisão por números de 2 dígitos:
1. Divida o seguinte:
(i) 8629 ÷ 12
(ii) 38245 ÷ 32
(iii) 16928 ÷ 11
(iv) 28724 ÷ 33
(v) 86458 ÷ 15
(v) 7542 ÷ 19
Responder:
1. (eu) Quociente: 719; Restante: 1
(ii) Quociente: 1195; Restante: 5
(iii) qUotient: 1538; Restante: 10
(4) Quociente: 870; Restante: 14
(v) Quociente: 5763; Restante: 13
(v) Quociente: 396; Restante: 18
Conceito relacionado
● Adição
● Problemas de palavras na adição
● Verifique se há subtração e adição
● Problemas de palavras envolvendo adição e subtração
● Estimando somas e diferenças
● Encontre os dígitos ausentes
● Multiplique um número por um número de 2 dígitos
● Multiplicação de um número por um número de 3 dígitos
● Problemas de palavras na multiplicação
● Divisão de dois dígitos por um número de um dígito
● Divisão de quatro dígitos por um número de um dígito
● Divisão por números de dois dígitos
● Problemas de palavras na divisão
Atividades matemáticas da 4ª série
Da divisão por números de dois dígitos para a página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.