Discutiremos aqui sobre a comparação de frações decimais.
Ao comparar os números naturais, comparamos primeiro o número whole de dígitos nos números e, se forem iguais, comparamos o dígito à extrema esquerda. Se eles também forem iguais, comparamos o próximo dígito e assim por diante. Seguimos o mesmo padrão enquanto comparamos os decimais.
✍️ Sabemos que um número decimal tem parte inteira e uma parte decimal. O número decimal com a maior parte inteira é maior.
Por exemplo, 5.4 é maior que 3,98.
✍️ Se todas as partes forem iguais, primeiro converta as decimais fornecidas em decimais e depois examine. Comparamos os dígitos no lugar dos décimos. O número decimal com o maior dígito no native dos décimos é maior.
Por exemplo, 9.85 é maior que 9,65.
✍️ Se os dígitos no native dos décimos forem iguais, examine os dígitos no native dos centésimos. O número decimal com o maior dígito no native dos centésimos é maior.
Por exemplo, 0,58> 0,55.
✍️Se os dígitos nos décimos e os centésimos lugares são os mesmos, o número decimal com o maior dígito no native da milésima parte será maior.
Por exemplo, 51.268> 51.265
Exemplos sobre a comparação de decimais:
1. Examine 0,6 e 0,8.
Solução:
0,6 = 6 décimos
0,8 = 8 décimos
Porque 8 décimos> 6 décimos
Assim, 0,8> 0,6
2. Examine 0,317 e 0,341
Solução:
0,317 = 0,3 + 0,01 + 0,007
= 3 décimos + 1 centésimos + 7 milésimos
0,341 = 0,3 + 0,04 + 0,001
= 3 décimos +4 centésimos + 1 milésimos
Porque 3 décimos = 3 décimos,
Agora, examine o próximo dígito
1 centésimos <4 centésimos
Assim, 0,317 <0,341
Etapas de comparação de frações decimais são dadas abaixo:
Etapa I: Primeiro, precisamos observar a parte integrante.
Por exemplo:
(i) 104 <140, é assim que verificamos a parte integral
(ii) 153 = 153
(iii) 112> 121
Etapa II: Quando a parte integral é a mesma, examine o lugar dos décimos
Por exemplo:
(i) 1.4 <1,9,
(ii) 1.5 = 1,50
(iii) 16.2> 16.1
Etapa III: Quando o décimo lugar é o mesmo que examine os centésimos.
Por exemplo:
(i) 10.04 <10.09,
(ii) 1,97 = 1,97
(iii) 71.92> 71,90
Dessa forma, primeiro verificamos a parte integral e depois passamos para os lugares decimais um por um.
Por exemplo:
1. O que é maior, 12.0193 ou 102.01?
Solução:
Primeiro verifique a parte inteira
12 e 102
12 é <102
102.01 é maior.
2. O que é menor, 19.023 ou 19.027?
Solução:
Para cada uma dessas decimais, a parte integrante é a mesma. Portanto, examine o lugar dos décimos. Também é o mesmo, verifique os centésimos lugares que também são os mesmos e depois passe para o próximo lugar decimal.
Portanto, 19.023 <19.027
Então, 19.023 é menor.
3. Encontre o número maior; 162.19 ou 126.91.
Solução:
162.19 é maior que 126,91.
4. Qual número é maior 293.82 ou 293.62?
Solução:
Primeiro verifique a parte inteira,
293 = 293
Então o décimo lugar
8> 6
Agora o centésimo lugar
2 = 2
Portanto, 293.82 é maior que 293,62.
5. Encontre o número maior; 1432.97 ou 1432.99
Solução:
Primeiro verifique a parte inteira,
1432 = 1432
Então o décimo lugar
9 = 9
Agora o centésimo lugar
7 <9
Portanto, 1432.99 é maior que 1432,97
6. Qual número é maior 187.653 ou 187.651?
Solução:
Primeiro verifique a parte inteira,
187 = 187
Então o décimo lugar
6 = 6
Então o centésimo lugar
5 = 5
Agora o milésimo lugar
3> 1
Portanto, 187.653 é maior que 187.651
7. Qual número é maior 153.017 ou 153.017?
Solução:
Primeiro verifique a parte inteira,
153 = 153
Então o décimo lugar
0 = 0
Então o centésimo lugar
1 = 1
Agora o milésimo lugar
7 = 7
Portanto, 153.017 = 153.017
8. Encontre o número maior; 1324.42 ou 1324.44
Solução:
Primeiro verifique a parte inteira,
1324 = 1324
Então o décimo lugar
4 = 4
Agora o centésimo lugar
2 <4
Portanto, 1324.44 é maior que 1324.42
9. Qual número é maior 804.07 ou 804.007?
Solução:
Primeiro verifique a parte inteira,
804 = 804
Então o décimo lugar
0 = 0
Então o centésimo lugar
7> 0
Portanto, 804.07 é maior que 804,007
10. Encontre o número maior; 211.21 ou 211.21
Solução:
Primeiro verifique a parte inteira,
211 = 211
Então o décimo lugar
2 = 2
Agora o centésimo lugar
1 = 1
Portanto, 211.21 = 211.21
11. Escreva em ordem crescente usando
(um) 43.81, 43.18, 43.08, 43.80
Solução:
43.08 <43,18 <43,80 <43,81
(b) 89.09, 89,90, 89.01, 89.03
Solução:
89.01 < 89.03 < 89.09 <89.90
(c) 53.35, 53.53, 53.30, 53.05
Solução:
53,05 <53,30 <53,35 <53,53
(D) 61.16, 61.61, 61.06, 61.36
Solução:
61.06 <61.16 <61,36 <61,61
12. Manage os seguintes números decimais em ordem ascendente.
9.02; 2.56; 2.66; 8.02
Solução:
A maior parte integral é 9. Portanto, 9.02 é o maior número no conjunto acima. 2.56 e 2.66 têm peças integrais iguais, comparamos os dígitos nos décimos lugar 5> 6. Então, 2,66> 2,56.
Os números decimais em ordem ascendente são 2,56; 2.66; 8.02; 9.02
13. Examine e coloque o sinal apropriado:
(i) 13,6 ______ 1,36
(ii) 65.010 ______ 65.110
(iii) 209.008 ______ 210.007
(iv) 47.981 ______ 29.999
Solução:
(i)>
(ii) <
(iii) <
(iv)>
Regras de trabalho para comparação de decimais:
Passo I: Examine todas as partes dos números fornecidos. O número com maior parte inteira será maior. Se todas as partes forem iguais, vá para o próximo passo.
Etapa II: Examine os dígitos extremos da esquerda das partes decimais de dois números. O número com maior dígito extremo esquerdo será maior. Se os dígitos extremos da esquerda das peças decimais forem iguais, examine os próximos dígitos e assim por diante.
Exemplos resolvidos:
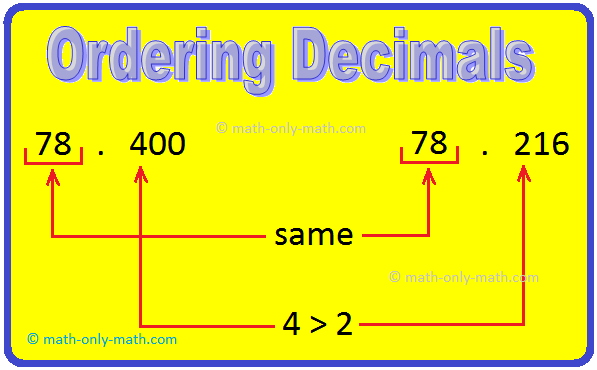
1. Qual decimal é maior 78,40 ou 78.216?
Solução:
Convertendo as decimais dadas em decimais semelhantes
78.40 = 78.400
78.216 = 78.216
Portanto, 78.400> 78.216
Assim, 78.40> 78.216
2. Qual é o maior 35.40 ou 35.209?
Solução:
Dados decimais, são 35,40 e 35.209.
Convertendo os decimais fornecidos em decimais semelhantes, temos
35.40 = 35.400
35.209 = 35.209
Portanto, 35.400> 35.209
Por isso, 35.40> 35.209
Responder:
Ao comparar os decimais, primeiro comparamos a parte do número inteiro (se houver). A parte decimal com maior número inteiro é maior e, se decimal, com menor parte do número inteiro for menor, comparamos a parte decimal de um número decimal se suas peças inteiras forem iguais
Por exemplo:
Examine os decimais.
(i) 3,43, 4.12
(ii) 6.87, 6.12
Solução:
(i) Examine todo o número da parte IE 3 <4
Então, 3,43 <4,12
(ii) as peças do número inteiro são iguais. Examine o primeiro lugar decimal
ou seja, 8 décimos> 1 décimos
Então, 6.87> 6.12
● Decimal.
Gráfico de valor de native decimal.
Forma expandida de frações decimais.
Ao contrário da fração decimal.
Frações decimais equivalentes.
Mudando diferente de gostar de frações decimais.
Comparação de frações decimais.
Conversão de uma fração decimal em um número fracionário.
Conversão de frações em números decimais.
Problemas na adição de frações decimais
Subtração de frações decimais.
Problemas na subtração de frações decimais
Multiplicação de números decimais.
Multiplicação de um decimal por um decimal.
Propriedades da multiplicação de números decimais.
Problemas na multiplicação de frações decimais
Divisão de um decimal por um número inteiro.
Divisão de frações decimais por múltiplos.
Divisão de um decimal por um decimal.
Divisão de um número inteiro por um decimal.
Propriedades da divisão de números decimais
Problemas na divisão de frações decimais
Conversão de fração em fração decimal.
Problemas de palavras em decimal.
Problemas de matemática da 5ª série
Da comparação de frações decimais à página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.