Um número fracionário cujo denominador é 10 ou múltiplo de 10 é chamado de decimal. Todo decimal tem duas partes de parte do número inteiro e parte decimal. Essas duas partes são separadas por um ponto ou ponto. Este ponto ou ponto é conhecido como ponto decimal.
Por exemplo, 51.731 é decimal. Aqui 51 é toda a parte e 731 é a parte decimal.
Nosso sistema de números de contagem possui 10 dígitos para escrever todos os números usando valores de lugar. Sabemos que a posição de um dígito no número determina seu valor no número. Cada native no gráfico de valor native é 10 vezes maior que o native à sua direita.
Por exemplo; 10 ONE = 1 dez, 10 dezenas = 1 cem, 10 centenas = 1 mil. Vamos agora estender a idéia de valor native desenvolvida para números inteiros para parte fracionária de um número inteiro. Os lugares à direita do native são chamados de lugares decimais. Cada native é dez vezes menor que o da esquerda imediata. Portanto, o valor do native de um dígito se torna ( frac {1} {10} ) quando movemos um lugar para a direita.
Como ler um decimal?
O comprimento de um lápis é de 17,2 cm. Isso é lido como dezessete pontos dois cm.
Um decimal é lido de duas maneiras:
(i) 43.814 é lido como quarenta e três pontos oito, um, quatro.
(ii) 43.814 é lido como quarenta e oitocentos e quatorze milésimos.
Como escrever um número fracionário como decimais?
7/10 = 0,07
2179/1000 = 2.179
Frações decimais
Algumas frações têm denominadores 10, 100, 1000 e assim por diante.
Por exemplo, ( frac {3} {10} ), ( frac {7} {100} ), ( frac {9} {1000} )
Podemos representar essas frações da seguinte maneira.
( frac {3} {10} ) = 0,3
( frac {7} {100} ) = 0,07
( frac {9} {1000} ) = 0,009
Tais frações são chamadas frações decimais.
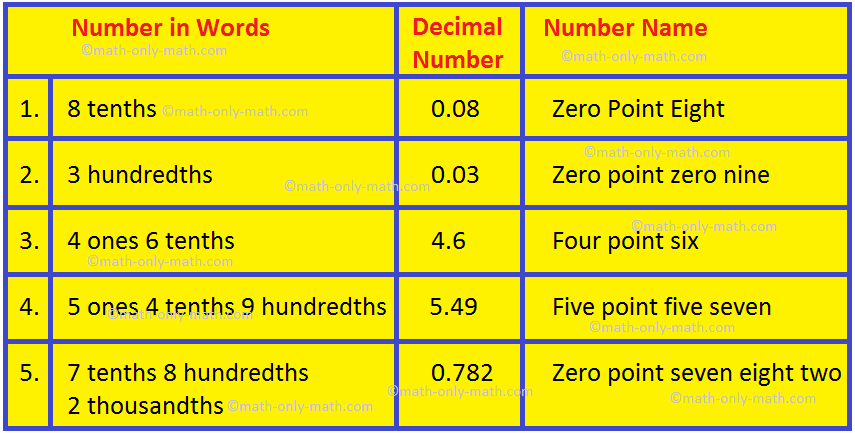
Escreva o número decimal na tabela abaixo:
Como escrever um decimal como números fracionários?
Para converter um número decimal 49.50 em uma fração, 49,50 = 4950/100.
De forma related,
(i) 1.1 = 11/10
(ii) 2.13 = 213/100
(iii) 17.2 = 172/10
(iv) 14.11 = 1411/100
(v) 9.781 = 9781/1000
Então, pela explicação acima, concluímos que o número está dividido:
(a) por 10 se houver um dígito após o decimal.
(b) por 100 se houver dois dígitos após o decimal.
(c) por 1000 se houver três dígitos após o decimal.
(d) por 10000 se houver três dígitos após o decimal e assim por diante.
(a) O número é dividido por 10 se houver um dígito após o decimal.
Por exemplo:
(i) 1.5 = 15/10
(Observamos que em 1.5, após o decimal, há um dígito, então precisamos dividir até 10)
(ii) 12.3 = 123/10
(Observamos que em 12.3, após o decimal, há um dígito, então precisamos dividir até 10)
(iii) 10.1 = 101/10
(Observamos que em 10.1, após o decimal, há um dígito, então precisamos dividir até 10)
(iv) 111.2 = 1112/10
(Observamos que em 111.2, após o decimal, há um dígito, então precisamos dividir até 10)
(v) 145.9 = 1459/10
(Observamos que em 145.9, após o decimal, há um dígito, então precisamos dividir até 10)
(b) O número é dividido por 100 se houver dois dígitos após o decimal.
Por exemplo:
(i) 2.51 = 251/100
(Observamos que em 2.51, após o decimal, há dois dígitos, então precisamos dividir por 100)
(ii) 12.03 = 1203/100
(Observamos que em 12.03, após o decimal, há dois dígitos, então precisamos dividir por 100)
(iii) 19.11 = 1911/100
(Observamos que em 19.11, após o decimal, há dois dígitos, então precisamos dividir por 100)
(iv) 11.24 = 1124/100
(Observamos que em 11.24, após o decimal, há dois dígitos, então precisamos dividir por 100)
(v) 14.93 = 1493/100
(Observamos que em 14,93, após o decimal, há dois dígitos, então precisamos dividir por 100)
(c) O número é dividido por 1000 se houver três dígitos após o decimal.
Por exemplo:
(i) 1.555 = 1555/1000
(Observamos que em 1.555, após o decimal, há três dígitos, então precisamos dividir por 1000)
(ii) 12.005 = 12005/1000
(Observamos que em 12.005, após o decimal, há três dígitos, então precisamos dividir por 1000)
(iii) 2.001 = 2001/1000
(Observamos que em 2,001, após o decimal, há três dígitos, então precisamos dividir por 1000)
(iv) 1.112 = 1112/1000
(Observamos que em 1.112, após o decimal, há três dígitos, por isso precisamos dividir por 1000)
(v) 15.913 = 15913/1000
(Observamos que em 15.913, após o decimal, há três dígitos, então precisamos dividir por 1000)
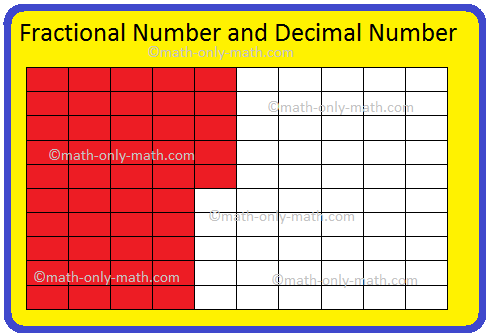
EU. Escreva o número fracionário e o número decimal para a parte sombreada da figura.
Vemos que a folha é dividida em 100 partes iguais. Cada parte representa cento e centésimos do todo.
Entre as 100 partes, a parte sombreada está 45.
Portanto, podemos representar a figura em forma fracionária como ( frac {45} {100} ) e em forma decimal como 0,45onde 4 representa 4 décimos e 5 representa 5 centésimos.
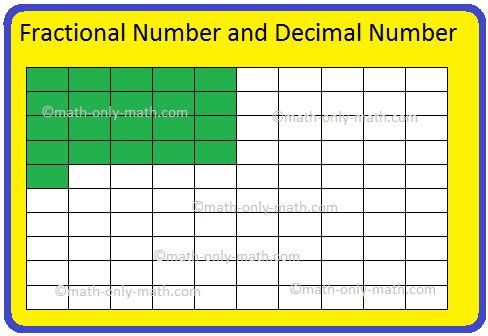
Ii. Escreva o número fracionário e o número decimal para a parte sombreada da figura.
Vemos que a folha é dividida em 100 partes iguais. Cada parte representa cento e centésimos do todo.
Entre as 100 partes, a parte sombreada está 21.
Portanto, podemos representar a figura em forma fracionária como ( frac {21} {100} ) e em forma decimal como 0,21onde 2 representa 2 décimos e 1 representa 1 centésimos.
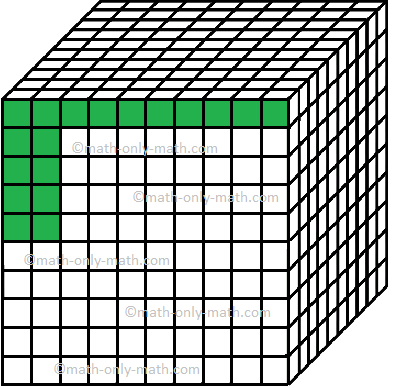
Iii. Escreva o número fracionário e o número decimal para a parte sombreada da figura.
Vemos que a folha é dividida em 1000 partes iguais. Cada parte representa cento e centésimos do todo.
Entre as 1000 partes, a parte sombreada é 18.
Portanto, podemos representar a figura em forma fracionária como ( frac {18} {1000} ) e em forma decimal como 0,018onde 0 representa 0 décimos, 1 representa 1 centésimos e 8 representa 8 milésimos.
Pratique problemas em decimais:
1. Nomeie os seguintes números decimais.
(i) 0,9
(ii) 197.33
(iii) 0,57
(iv) 72.465
(v) 35.064
(vi) 84.06
Respostas:
(i) Zero Level Nove
(ii) cento e noventa e sete pontos três três
(iii) ponto zero cinco sete
(iv) setenta e dois pontos quatro seis cinco
(v) trinta e cinco pontos zero seis quatro
(vi) Oitenta e quatro pontos zero seis
Problemas de matemática da 5ª série
Da 5ª série decimais à página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.