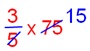Problemas de palavras na fração | Problemas de palavra da fração matemática | matemática de fração

Em problemas de palavras na fração, resolveremos diferentes tipos de problemas na multiplicação de números fracionários e divisão de números fracionários.

I. Problemas de palavras na adição de frações:

1. Nairitae levou ( frac {7} {8} ) hora para pintar uma mesa e ( frac {2} {3} ) hora para pintar uma cadeira. Quanto tempo ele levou para pintar os dois itens?

Solução:

Tempo whole gasto na pintura de ambos os itens = ( frac {7} {8} ) h + ( frac {2} {3} ) h
= ( ( frac {7} {8} ) + ( frac {2} {3} )) h

= ( ( frac {21 + 16} {24} )) h

= ( frac {37} {24} ) h

= 1 ( frac {13} {24} ) h

Portanto, o Nairitae levou 1 ( frac {13} {24} ) horas na pintura de ambos os itens.

2. Nitheeya e Nairitee ( frac {3} {10} ) e ( frac {1} {6} ) de um bolo, respectivamente. Que parte do bolo eles comeram juntos?

Solução:

A parte do bolo comia por nitheeya = ( frac {3} {10} )

A parte do bolo comia por nitheeya = ( frac {1} {6} )

A parte que eles comeram juntos = ( frac {3} {10} ) + ( frac {1} {6} )

= ( frac {9} {30} ) + ( frac {5} {30} ); (Desde, LCM de 10 e 6 = 30)

= ( frac {9 + 5} {30} )

= ( frac {14} {30} )

= ( frac {7} {15} )

Portanto, juntos nitheeya e nairitae comeram ( frac {7} {15} ) do bolo.

3. Rachel levou ( frac {1} {2} ) hora para pintar uma mesa e ( frac {1} {3} ) hora para pintar uma cadeira. Quanto tempo ela levou em tudo?

Solução:

Ii. Problemas de palavras na subtração de frações:

1. Fora de ( frac {12} {17} ) m de pano dado a um alfaiate, ( frac {1} {5} ) m foram usados. Encontre o comprimento do pano sem uso.

Solução:

Comprimento do pano dado aos alfaiates = ( frac {12} {17} ) m

Comprimento do pano usado = ( frac {1} {5} ) m

Comprimento do pano não utilizado = ( frac {12} {17} ) M – ( frac {1} {5} ) m

= ( ( frac {12} {17} ) – ( frac {1} {5} )) m

= ( ( frac {12 × 5} {17 × 5} ) – ( frac {1 × 17} {5 × 17} )) m; (Desde, LCM de 17 e 5 = 85)

= ( ( frac {60} {85} ) – ( frac {17} {85} )) m

= ( ( frac {60 – 17} {85} ) m

= ( ( frac {43} {85} ) m

2. Nairitae possui $ 6 ( frac {4} {7} ). Ela fornece $ 4 ( frac {2} {3} ) para sua mãe. Quanto dinheiro ela tem agora?

Solução:

Dinheiro com Nairitee = $ 6 ( frac {4} {7} )

Dinheiro dado a sua mãe = $ 4 ( frac {2} {3} )

Dinheiro deixado com Nairitee = $ 6 ( frac {4} {7} ) – $ 4 ( frac {2} {3} )

= $ (6 ( frac {4} {7} ) – 4 ( frac {2} {3} ))

= $ ( ( frac {46} {7} ) – ( frac {14} {3} ))

= $ ( ( frac {46 × 3} {7 × 3} ) – ( frac {14 × 7} {3 × 7} )); (Desde, LCM de 7 e 3 = 21)

= $ ( ( frac {138} {21} ) – ( frac {98} {21} ))

= $ ( frac {40} {21} )

= $ 1 ( frac {19} {21} )

Portanto, o Nairitae possui $ 1 ( frac {19} {21} ).

3. Se 3 ( frac {1} {2} ) m de fio é cortado a partir de um pedaço de fio de 10 m de comprimento, quanta fios é deixada?

Comprimento whole do fio = 10 m

Fração do fio cortado = 3 ( frac {1} {2} ) m = ( frac {7} {2} ) m

Comprimento do fio esquerdo = 10 m – 3 ( frac {1} {2} ) m

= ( ( frac {10} {1} ) – ( frac {7} {2} )) m, (lcm de 1, 2 é 2)

= ( ( frac {20} {2} ) – ( frac {7} {2} )) m, ( ( frac {10} {1} ) × ( frac {2} {2} ))

= ( ( frac {20 – 7} {2} )) m

= ( frac {13} {2} ) m

= 6 ( frac {1} {2} ) m

Iii. Problemas de palavras na multiplicação de frações:

1. ( frac {4} {7} ) de um número é 84. Encontre o número.

Solução:

De acordo com o problema,

( frac {4} {7} ) de um número = 84

Número = 84 × ( frac {7} {4} )

(Aqui precisamos multiplicar 84 pelo recíproco de ( frac {4} {7} ))

= 21 × 7

= 147

Portanto, o número é 147.

2. Metade dos alunos de uma escola são meninas, ( frac {3} {5} ) dessas meninas estão estudando em courses mais baixas. Que fração das meninas estão estudando em courses mais baixas?

Solução:

Fração de meninas estudando na escola = ( frac {1} {2} )

Fração de meninas estudando em courses mais baixas = ( frac {3} {5} ) de ( frac {1} {2} )

= ( frac {3} {5} ) × ( frac {1} {2} )

= ( frac {3 × 1} {5 × 2} )

= ( frac {3} {10} )

Portanto, ( frac {3} {10} ) das meninas que estudam em courses mais baixas.

3. Maddy lê três quintos de 75 páginas de sua lição. Quantas páginas mais ele precisa para concluir a lição?

Solução:

Maddy lê = ( frac {3} {5} ) de 75

= ( frac {3} {5} ) × 75

= 45 páginas.

Maddy tem que ler = 75 – 45.

= 30 páginas.

Portanto, Maddy tem que ler mais 30 páginas.

4. Nitheeya caminha 2 ( frac {1} {2} ) Km Distância em uma hora. Quantos quilômetros ela pode andar em 8 ( frac {1} {4} ) horas?

Solução:

Distância caminhada em 1 hora = 2 ( frac {1} {2} )

A distância pode ser passada em 8 ( frac {1} {4} ) horas

= 8 ( frac {1} {4} ) * 2 ( frac {1} {2} ) km

= ( frac {8 × 4 + 1} {4} ) * ( frac {2 × 2 + 1} {2} )

= ( frac {33} {4} ) * ( frac {5} {2} )

= ( frac {33 × 5} {4 × 2} )

= ( frac {165} {8} )

= 20 ( frac {5} {8} ) km

4. Problemas de palavras na divisão de frações:

1. Um rebanho de vacas dá 4 litros de leite todos os dias. Mas cada vaca dá um terço do leite whole a cada dia. Eles dão 24 litros de leite em seis dias. Quantas vacas existem no rebanho?

Solução:

Um rebanho de vacas dá 4 litros de leite todos os dias.

Cada vaca fornece um terço do leite whole a cada dia = ( frac {1} {3} ) de 4

Portanto, cada vaca fornece ( frac {4} {3} ) do leite a cada dia.

Whole não. de vacas = 4 ÷ ( frac {4} {3} )

= 4 × ( frac {3} {4} )

= 3

Portanto, existem 3 vacas no rebanho.

Planilha sobre problemas de palavras sobre frações:

1. Shelly andou ( frac {1} {3} ) km. Kelly andou ( frac {4} {15} ) km. Quem caminhou mais longe? Quanto mais um caminhou do que o outro?

2. Um sapo deu três saltos. O primeiro salto foi ( frac {2} {3} ) m de comprimento, o segundo foi ( frac {5} {6} ) m de comprimento e o terceiro foi ( frac {1} {3} ) m de comprimento. Até onde o sapo saltou?

3. Um navio contém 1 ( frac {1} {2} ) l do leite. John Drinks ( frac {1} {4} ) l do leite; Joe Drinks ( frac {1} {2} ) l do leite. Quanto de leite resta no navio?

4. Entre 4 ( frac {2} {3} ) e 3 ( frac {2} {3} ) que é maior e quanto?

5. O que deve ser subtraído de 5 ( frac {1} {6} ) para obter 2 ( frac {1} {8} )?

● A multiplicação é uma adição repetida.

● Multiplicação do número fracionário por um número inteiro.

● Multiplicação de uma fração por fração.

● Propriedades da multiplicação de números fracionários.

● Inverso multiplicativo.

● Planilha sobre multiplicação sobre fração.

● Divisão de uma fração por um número inteiro.

● Divisão de um número fracionário.

● Divisão de um número inteiro por uma fração.

● Propriedades da divisão fracionária.

● Planilha sobre Divisão de Frações.

● Simplificação de frações.

● Planilha sobre simplificação de frações.

● Problemas de palavras na fração.

● Planilha sobre problemas de palavras em frações.

Números da 5ª série

Problemas de matemática da 5ª série

De problemas de palavras na fração para a página inicial