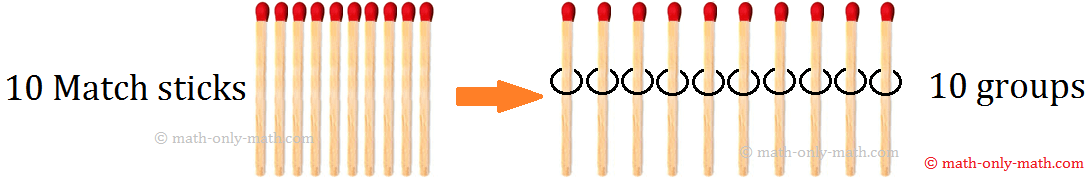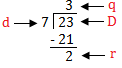Já aprendemos a divisão por subtração repetida, compartilhamento/distribuição igual e método de divisão curta. Agora, leremos alguns fatos sobre a divisão para aprender longa divisão.
I: Dividindo um número por 0:
1. Se o dividendo for ‘zero’, qualquer número como divisor dará o quociente como ‘zero’.
Por exemplo: Se os doces ‘zero’ forem distribuídos entre 8 crianças, naturalmente ninguém receberá doces.
II: Dividindo um número por 1:
2. Se o divisor for ‘1’, qualquer dividendo terá o quociente igual a si mesmo.
Quantas partidas ficam no grupo?
Obviamente, existem 10 Match Sticks no grupo.
Podemos escrever isso como 10 ÷ 1 = 10.
Quando dividimos um número por 1, o quociente é o próprio número.
Por exemplo: 4 ÷ 1 = 4
15 ÷ 1 = 15
50 ÷ 1 = 50
Por exemplo: Existem 15 doces; Cada criança deve obter 1 doce. Quantas crianças recebem os doces?

III: Dividindo um número por si só:
3. Quando dividimos 0 por um número, o quociente é sempre 0.
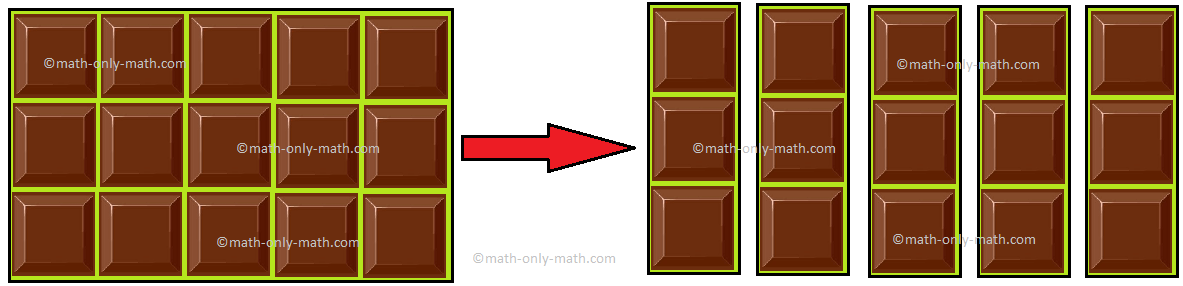
Quantos Match Sticks em cada grupo?
Podemos ver que existe 1 Match Stick em cada grupo.
Podemos escrever isso como
10 ÷ 10 = 1
Quando dividimos um número por si só, o quociente é sempre 1.
Por exemplo: 4 ÷ 4 = 1
15 ÷ 15 = 1
50 ÷ 50 = 1
IV: Dividindo 0 por um número:
4. Quando dividimos 0 por um número, o quociente é sempre 0.
Por exemplo: 0 ÷ 4 = 0
0 ÷ 15 = 0
0 ÷ 50 = 0
5. O produto do divisor e o quociente adicionado ao restante são sempre iguais ao dividendo.
(Divisor × quociente) + restante = dividendo.
(d × q) + r = d
Observação:
Sempre encontre o produto primeiro e adicione o restante. (Isso nos ajuda a verificar se a divisão é feita correta ou não.)
Exemplo: Divida 23 por 7
Verificação:
(d × q) + r = d
(7 × 3) + 2 = 23
21 + 2 = 23
23 = 23
Então, a divisão está correta.
6. Em uma soma de divisão, o restante é sempre menor que o divisor.
Exemplo:
No último exemplo, claramente podemos ver que o restante (2) é menor que o divisor (7).
7. Todo fato divisor tem dois fatos de multiplicação para verificá -lo.
Exemplo:
Na divisão, 12 ÷ 6 = 2, dois fatos de multiplicação são 2 × 6 = 12 e 6 × 2 = 12.
8. O quociente e o divisor são sempre os fatores do dividendo, se não houver restante.
Exemplo:
9. O dividendo é sempre um múltiplo do quociente e divisor, se não houver restante.
Exemplo:
|
D 30 5 6 |
÷ × × |
d 5 6 5 |
= = = |
q 6 30 30 |
Vamos fazer uma rápida revisão do que aprendemos sobre a divisão. A divisão está dividindo em partes ou grupos iguais. É o resultado de “compartilhamento justo”.
Se 5 amigos querem compartilhar 15 candies. Quantos candies cada um deles terá? Vamos dividir os candies igualmente entre eles.
15 divididos por 5 é 3. Eles recebem 3 cada.
Divisão com restante
Quando o número fornecido de coisas não pode ser compartilhado igualmente, algo resta. Isso é chamado de restante.
Exemplo:
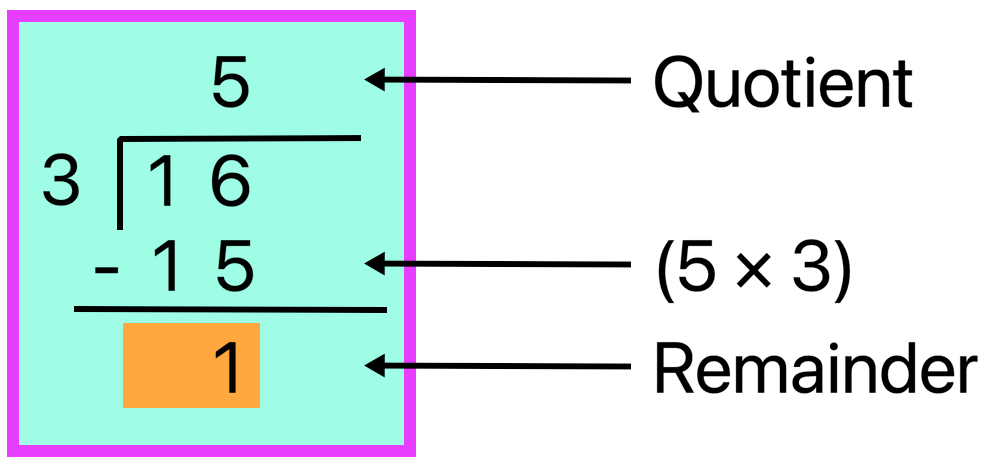
Divida 16 caramelo entre três filhos.
Solução:
Como 1 é menor que 3, então tomamos 16 como dividendos
3 × 5 = 15
Escreva 15 abaixo de 16 e subtraia
16 – 15 = 1
Então, quociente 5, restante = 1
Portanto, cada criança recebe 5 caramelos e 1 caramelo é deixado.
RESUMO
• Em uma soma de divisão como 15 ÷ 3 = 5, 15 é chamada de dividendo, 3 é chamado de divisor e 5 é chamado de quociente.
• O número que é deixado individido em divisão é chamado de restante.
• Quando 0 é dividido por um número, o quociente é 0.
• Quando um número é dividido por 1, o quociente é o próprio número.
• A divisão por 0 não tem significado.
Planilha sobre fatos sobre a divisão:
1. Preencha os números ausentes:
(i) 5 ÷ 1 = _____
(ii) 0 ÷ 8 = _____
(iii) 17 ÷ _____ = 1
(iv) _____ ÷ 1 = 9
(v) _____ ÷ 19 = 0
(vi) 81 ÷ _____ = 1
(vii) 14 ÷ _____ = 14
(viii) 26 ÷ 26 = _____
(ix) _____ ÷ 99 = 1
Responder:
1. (i) 5
(ii) 0
(iii) 17
(iv) 9
(v) 0
(vi) 81
(vii) 1
(viii) 1
(ix) 99
Aulas de matemática da 3ª série
De fatos sobre a divisão para a página inicial
Não encontrou o que você estava procurando? Ou quero saber mais informações sobre Somente matemática.
Use esta pesquisa do Google para encontrar o que você precisa.