
Figura 1: Uma mola furtiva, objeto do experimento da gota furtiva. Atribuição: Roger McLassus. CC BY-SA
A queda furtiva é um experimento bastante simples. Na sua forma mais básica, requer apenas um brinquedo fashionable para crianças, uma mão estável e um olhar atento. Para uma melhor visualização, usar um smartphone moderno para capturar um vídeo do experimento também ajuda a capturar a mola em queda. Além do resultado comumente citado, o Perception discutirá a evolução da forma furtiva durante a queda usando apenas a física do ensino médio: equilíbrio mecânico e a conservação do momento.
O que é o experimento Slinky Drop?
O experimento da queda furtiva é exatamente o que parece:
- Apoie uma mola em uma de suas pontas. Deixe o resto pendurado livremente sob a gravidade até atingir o equilíbrio.
- Solte o furtivo!
- Observe como ele cai sob a influência da gravidade e de forças internas. Preste atenção especial ao movimento da extremidade inferior.
O resultado do experimento é bastante impressionante e surpreendente para muitos. Se você deseja experimentar antes de prosseguirmos, pare de ler agora!
Resultados
Imediatamente após o lançamento, a extremidade inferior da mola permanece imóvel por algum tempo. Isso dura até que a perturbação criada pela liberação da extremidade superior atinja a extremidade inferior. Se você não tinha meios ou vontade de experimentar, há um vídeo fashionable da Veritasium:
A explicação para a extremidade inferior permanecer estacionária está no vídeo, mas resumimos para completar: Enquanto o segmento da mola emblem acima da extremidade permanece esticado, ele atua na parte last com a mesma força de antes da queda. Esta é exatamente a força necessária para equilibrar a gravidade quando a mola foi liberada do equilíbrio. Como resultado, a parte inferior permanece estacionária até que a perturbação a atinja. Simplesmente não importa o que aconteça mais acima na mola furtiva até que a perturbação passe.
Analisando a queda furtiva
Embora a explicação seja incontroversa, há alguma ambigüidade como a perturbação. Algumas fontes parecem sugerir que uma onda de compressão common desce pela mola. No entanto, existem vários problemas com esse modelo, incluindo não combinar muito bem com o formato furtivo durante o outono. Em certo sentido, esta é uma ótima notícia! Para compreender verdadeiramente tal onda, teríamos que derivar e resolver a equação de onda do furtivo. Esta é uma tarefa que seria adequada para estudantes do segundo ou terceiro ano de física universitária.
Em vez de uma onda de compressão common e da resolução da equação da onda, a física da queda furtiva é relativamente simples. Na verdade, um modelo muito bom pode ser compreendido usando os conceitos básicos da física do ensino médio. A análise abaixo apresenta primeiro a configuração da estrutura matemática. Em seguida, continua a discutir a forma de equilíbrio da mola furtiva e, finalmente, discute a dinâmica da queda.
Configurar
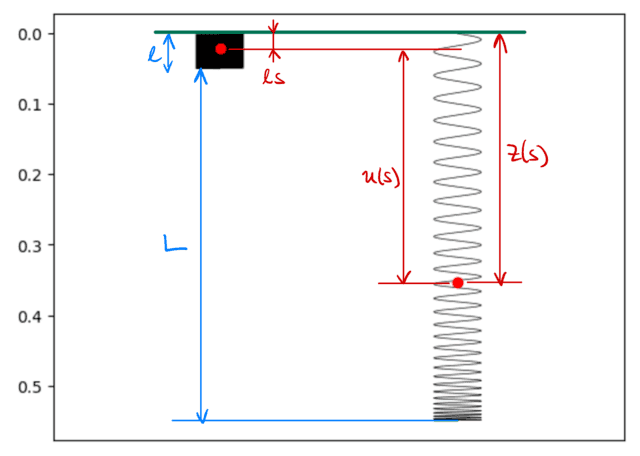

Figura 2: Configuração da descrição furtiva. A mola esquerda tem seu comprimento de descanso ##ell## e a direita fica pendurada sob a influência da gravidade. O ponto vermelho representa o mesmo ponto materials em ambos os casos.
Modelamos o furtivo como uma mola elástica de comprimento de repouso ##ell## e massa ##m##. Introduzimos uma coordenada vertical ##z## tal que a extremidade superior da mola é mantida em ##z = 0## e a coordenada aumenta na direção para baixo. Além disso, introduzimos ##s## como uma coordenada que descreve a fração do furtivo acima de um ponto específico. Na ausência de gravidade, o furtivo estaria em repouso. A posição ##z(s)## de um ponto na corda é então: $$z(s) = ell s$$ A posição ##z(s)## quando esticada geralmente está na forma $ $z(s) = ell s + u(s).$$ Aqui, ##u(s)## é o deslocamento da posição de repouso e será nosso foco a partir de agora. Uma representação gráfica da configuração é mostrada na Figura 2.
O Slinky em Equilíbrio
De acordo com a lei de Hooke, a tensão ##T(s)## na mola furtiva na fração de corda ##s## é proporcional à deformação ##u'(s)##. Matematicamente, isso implica que $$T(s) = alpha u'(s),$$ com ##alpha## sendo uma constante. Para encontrar o equilíbrio da mola suspensa, podemos agora fazer um diagrama de corpo livre da parte da mola abaixo de ##s##.
Duas forças atuam nesta parte: a força ##T(s)## devido à tensão e à gravidade. Com a massa abaixo de ##s## sendo dada por ##m(1-s)## e as forças se equilibrando, devemos ter $$T(s) = alpha u'(s) = mg(1 -s).$$ Integrando isso e usando ##u(0) = 0## (já que a extremidade superior é fixada em ##z = 0##) leva a $$u(s) = frac{mg} {alfa} sleft( 1 – frac s2right) = 2Lsleft( 1 – frac s2right) equiv u_0(s).$$ Acima, a nova constante ##L = u(1) = mg/2alpha# #, que é o alongamento complete da mola em equilíbrio, foi introduzido.
Duas seções do Slinky
Uma vez liberada, a parte superior da mola começa a cair imediatamente. A parte inferior permanece estacionária até que a perturbação a atinja. A captura de vídeo de um slinky caindo sugere que a parte superior se transfer como uma só, essencialmente na configuração de repouso do slinky, uma vez que a perturbação tenha passado. Isto sugere que a parte acima da frente de perturbação colide continuamente de forma inelástica com a próxima parte da mola furtiva.
Descrevendo matematicamente o que foi dito acima, seja ##s = sigma







