Discover frações com esta lição interativa
Clique em qualquer fração ou crie a sua própria para ver como ela fica como parte de todo o círculo!
Fração: 0/1
O que são frações?
As frações são usadas para indicar o número de partes de um todo. Suponha que você vá à pizza Domino’s e peça uma pizza média. Se a sua pizza tiver 8 fatias e você não comeu a pizza inteira, isso significa que partes da pizza inteira ficarão na caixa da pizza.
A pizza da esquerda mostra seis oitavos (6/8) e a pizza da direita mostra quatro oitavos (4/8).
6/8 e 4/8 são chamados de frações.
O número superior é o numerador da fração e nos diz quantas fatias existem.
O número inferior é o denominador da fração e nos diz quantas fatias iguais existem no complete.
Da mesma forma, suponha que um retângulo tenha 4 partes iguais e sombreemos 1 parte do retângulo. A fração é 1/4
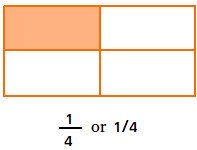
Observe que uma barra (/) ou uma linha horizontal podem ser usadas para separar o numerador do denominador. Como a linha horizontal é mais atraente, preferimos usá-la em vez de uma barra.
2
8
=
2/8
Frações equivalentes
Agora, dê uma olhada na figura abaixo. Você pode ver claramente que seis oitavos (6/8) de uma pizza inteira é igual a três quartos (3/4) de uma pizza inteira.
6/8 e 3/4 são frações equivalentes. Embora 6/8 e 3/4 tenham numeradores e denominadores diferentes, ambos são iguais.
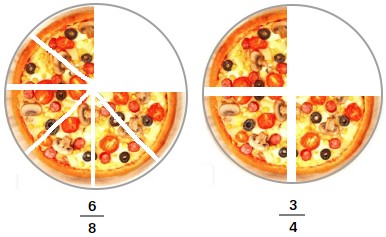
Na verdade, 6/8 = 3/4 = 0,75
Mais exemplos de frações equivalentes
4
8
=
1
2
5
10
=
1
2
5
15
=
1
3
Termos superiores e termos inferiores de frações
Observe que para ir de 1/2 a 4/8, tudo o que precisamos fazer é multiplicar o numerador e o denominador de 1/2 pelo mesmo número ou 4.
Da mesma forma, para ir de 1/3 a 5/15, podemos multiplicar o numerador e o denominador de 1/3 por 5.
4/8 e 5/15 são chamados de termos superiores de 1/2 e 1/3, respectivamente.
Tome cuidado! 4/8 não é maior que 1/2 e 5/15 não é maior que 1/3.
4/8 é um termo superior a 1/2 apenas porque tem um numerador maior e um denominador maior. Porém, vimos antes que 1/2 e 4/8 são frações equivalentes, pois 1/2 = 4/8 = 0,5
Observe também que você pode passar de um termo superior para um termo inferior. Por exemplo, para reduzir 5/15 a um termo inferior, tudo o que você precisa fazer é dividir o numerador e o denominador por 5. Você obterá 1/3.
Simplificar uma fração é o processo de passar de termos superiores para termos inferiores. Para obter a forma mais simples de uma fração, divida o numerador e o denominador pelo maior fator comum (gcf) ou o maior número que se divide igualmente no numerador e no denominador.
Por exemplo, para trazer 10/40 ao seu valor mais simples, divida 10 e 40 por 10. Você obterá 1/4.
1/2 e 1/3 são os termos mais baixos de 4/8 e 5/15, respectivamente.
Adicionando frações
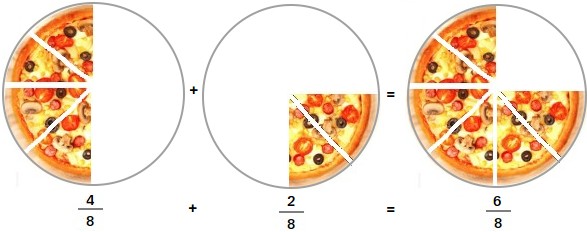
Quando as frações tiverem denominador comum (mesmo denominador), some os numeradores e mantenha o mesmo denominador.
4/8 + 2/8 = (4 + 2)/8 = 6/8
Observe que 1/2 = 4/8 e 1/4 = 2/8. Portanto, 1/2 + 1/4 = 4/8 + 2/8 = 6/8.
Se os denominadores não forem iguais, você precisará procurar o mínimo múltiplo comum (MCM) dos denominadores. Ver adicionando frações para mais explicações.
Usando frações para mostrar proporções
Você pode usar uma fração para mostrar uma proporção. Numa proporção, o numerador mostra a parte de um grupo que você está considerando e o denominador mostra o resto do grupo ou todo o grupo.
Suponha que uma turma tenha 6 meninos e 10 meninas. Qual é a proporção de meninos para meninas. Neste exemplo, o numerador é o número de meninos e o denominador é o resto do grupo ou o número de meninas.
A proporção de meninos para meninas é
6
10
Qual é a proporção de meninas em relação ao número complete de alunos? Neste caso, o numerador é o número de meninas e o denominador é todo o grupo ou o número complete de alunos.
A proporção de meninas em relação ao número complete de alunos é
10
16
Usando frações para mostrar divisão
Uma fração também pode ser usada para representar a divisão.
A expressão
4
5
também pode significar 4 dividido por 5 ou 4 ÷ 5
Você pode então escrever a fração como um decimal. Por exemplo, 4/5 = 4 ÷ 5 = 80/100 = 0,8
Frações de referência
Frações de referência são frações muito usadas em matemática básica e também são úteis para representar outras frações.
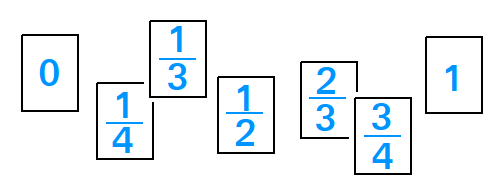
Com frações de referência, você pode fazer o seguinte:
- Examine e ordene frações rapidamente. Por exemplo, 2/3 é maior que 1/4.
- Frações redondas e números mistos. Por exemplo, 3/4 é arredondado para 1, pois está mais próximo de 1 do que de 0.
- Estime somas e diferenças de frações e números mistos. Por exemplo, 3/4 + 1/3 é maior que 1, pois 1/3 é maior que 1/4.
Alguns exemplos que mostram como as frações são usadas na vida cotidiana
1. Se você cozinha muito seguindo uma receita, então deve ter usado muito frações antes.
Suponha que uma receita diga para usar 12 colheres de sopa de açúcar para fazer um bolo de 3 quilos. Quanto açúcar você usará para um bolo de meio quilo?
Como você está fazendo 1/3 do bolo inteiro, você pode pensar que precisa usar 1/3 de 12 colheres de sopa.
2. Enfermeiros e farmacêuticos devem ser absolutamente bons em frações para dar ao paciente a dosagem correta de um medicamento. Suponha que a dosagem de um medicamento seja de 100 mg. Se o médico prescrever 25 mg, quantos comprimidos você administrará? Enfermeiros e farmacêuticos podem precisar da seguinte fórmula para resolver este problema,
Número de comprimidos a administrar
=
Força da medicação prescrita pelo médico
Dosagem de 1 comprimido
Número de comprimidos a administrar
=
25mg
100mg
Enfermeiros e farmacêuticos devem saber que 25/100 e 1/4 são frações equivalentes para que possam dar 1/4 do comprimido ao paciente.







