“E se a física NÃO estiver descrevendo a realidade”

Espaço-Tempo PBS produz alguns vídeos muito bons sobre os fundamentos da mecânica quântica (QM), então deixe-me comentar sobre o vídeo deles E se a física NÃO estiver descrevendo a realidade para fornecer informações faltantes (cruciais). Este comentário refere-se apenas aos primeiros 9 minutos do vídeo, ou seja, não tem nada a ver com “incerteza entrópica”, então você não precisa assistir mais do que isso antes de ler meu comentário. Depois de ler meu comentário, espero que você perceba que a física do programa de reconstrução quântica (definida abaixo) está bem fundamentada na realidade.

Em 1996, Rovelli desafiou físicos (1) para derivar o formalismo da MQ a partir de “princípios e postulados físicos”, como Einstein derivou as transformações de Lorentz da relatividade especial (SR) do princípio da relatividade e do postulado da luz. Houve muitos que aceitaram o desafio, um dos quais foi Zeilinger e o seu Princípio Basic da Qualidade da Qualidade em 1999 (2). Hardy seguiu com “Teoria Quântica a partir de Cinco Axiomas Razoáveis” em 2001 e houve muitos outros a caminho das “primeiras reconstruções totalmente rigorosas e completas” por Chiribella, D’Ariano e Perinotti (3) e Masanes e Mueller (4) em 2010-11 (com muitos mais depois disso). Esta reconstrução axiomática da MQ baseada em princípios da teoria da informação (programa de reconstrução quântica) conseguiu tornar a MQ uma “teoria de princípios” exatamente como a RS segundo o desafio de Rovelli.

(Nós explicamos tudo isso para o “leitor comum” em nosso livro, “O emaranhado de Einstein: desigualdades de Bell, relatividade e o Qubit” Oxford UP (2024), este comentário é apenas um resumo.)

Uma “teoria de princípio” de Einstein é aquela cujo formalismo decorre de um fato descoberto empiricamente (5). SR é uma teoria de princípio porque sua cinemática (transformações de Lorentz) segue de um fato descoberto empiricamente chamado postulado da luz, ou seja, todos medem o mesmo valor para a velocidade da luz cindependentemente de seus movimentos relativos. Desde c é uma constante da Natureza de acordo com o eletromagnetismo de Maxwell, o princípio da relatividade – as leis da física (para incluir suas constantes da Natureza) são as mesmas em todos os referenciais inerciais – diz que deve ser o mesmo em todos os referenciais inerciais. E, uma vez que os referenciais inerciais estão relacionados por movimentos relativos uniformes (impulsos), o princípio da relatividade nos diz que o postulado da luz deve ser obtido, daí as transformações de Lorentz do SR.

Da mesma forma, o programa de reconstrução quântica mostrou que a cinemática do QM (espaço de Hilbert de dimensão finita) segue de um fato descoberto empiricamente chamado “Invariância e Continuidade da Informação”:

A informação complete de um bit é invariante sob uma mudança contínua entre diferentes conjuntos completos de medições mutuamente complementares.

qual Brukner e Zeilinger ampliado do Princípio Fundacional de Zeilinger em 2009 (6). Em termos leigos, isso significa simplesmente que todos medem o mesmo valor para a constante de Planck hindependentemente de suas orientações espaciais relativas (deixe-me chamar isso de “postulado de Planck”). Desde h é uma constante da natureza pela lei de radiação de Planck, e os referenciais inerciais estão relacionados por diferentes orientações espaciais (rotações), esse fato descoberto empiricamente pode ser justificado com o princípio da relatividade exatamente como o postulado da luz do SR.

A superposição quântica é uma consequência do postulado de Planck e leva à conservação “apenas média”, que é responsável pelas correlações de emaranhamento quântico que violam a desigualdade de Bell. No entanto, uma vez que você entender como a conservação ‘somente média’ segue da superposição quânticaque decorre do postulado de Planck, que decorre do princípio da relatividade e da lei de radiação de Planck, não há nada de misterioso nas correlações de QM que violam a desigualdade de Bell. Veja como essas correlações fazem todo sentido usando spin-1/2 (conforme mostrado no vídeo).

Suponha que você envie um elétron de spin vertical para ímãs de Stern-Gerlach (SG) orientados a 60 graus em relação à vertical (Figura 1, como o vídeo onde eles enviaram os elétrons de spin vertical para ímãs SG horizontais).

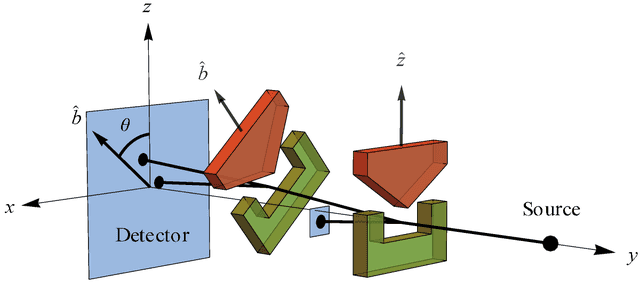
Figura 1

Como o spin é uma forma de momento angular, a mecânica clássica diz que a quantidade de momento angular vertical +1 que você deve medir a 60 graus é +1*cos(60) = 1/2 (em unidades de ##hbar## /2, Figura 2).

Figura 2

Mas, a medição SG do spin do elétron constitui uma medida de hentão todos precisam obter o mesmo ##pm##1 para uma medição de spin em qualquer orientação espacial SG, o que significa que você não pode obter o que espera da mecânica clássica do bom senso. Em vez disso, QM diz que a medição de um elétron spin up vertical a 60 graus produzirá +1 com uma probabilidade de 0,75 e produzirá -1 com uma probabilidade de 0,25, então a média é (+1 + 1 + 1 – 1) /4 = 1/2. Em outras palavras, QM diz que você obtém o resultado clássico do senso comum em ‘apenas média’ por causa da independência do observador de h. (Esta é a fonte de indeterminação em QM.) Isto explica o resultado mostrado no vídeo. Ou seja, QM diz que a medição de um elétron spin-up vertical a 90 graus produzirá +1 com uma probabilidade de 0,50 e produzirá -1 com uma probabilidade de 0,50, então a média é (+1 + 1 – 1 – 1)/4 = 0 = +1*cos(90).

Agora suponha que Alice e Bob estejam medindo o estado de spin singleto (os dois spins são anti-alinhados quando medidos na mesma direção, como mostrado no vídeo) e Alice obtenha +1 verticalmente e Bob mede sua partícula a 120 graus em relação a Alice ( Figuras 3 e 4). Se Bob tivesse medido verticalmente, ele teria obtido -1, então a 120 graus Alice diz que ele deveria obter 1/2 de acordo com nosso exemplo de partícula única.

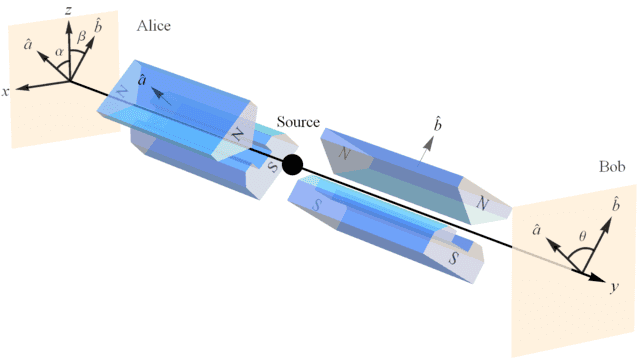
Figura 3

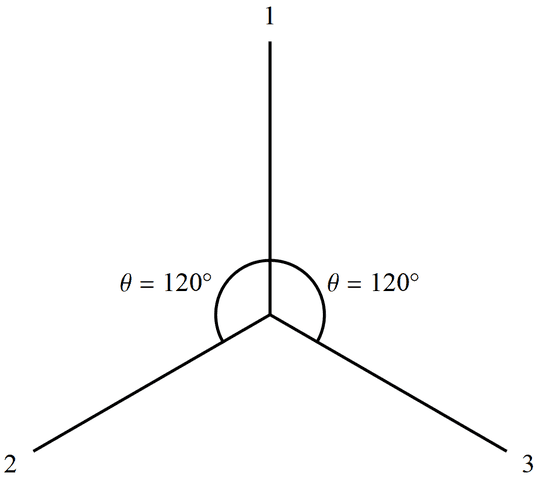
Figura 4

Mas é claro que Bob deve medir o mesmo valor para h que Alice faz, então ele não pode obter o valor fracionário de h Alice diz que deveria (caso contrário, Alice estaria em um referencial preferencial). Em vez disso, seus resultados a 120 graus correspondem aos resultados +1 de Alice, com média vertical de 1/2, assim como no caso de partícula única. E, claro, os dados são simétricos para que Bob possa particionar os resultados de acordo com dele ##pm##1 resultados e mostram que os resultados de Alice satisfazem a conservação do momento angular de spin na ‘média apenas’ quando estão em referenciais diferentes (fazendo medições diferentes). Portanto, Alice particiona os dados de acordo com seus resultados ##pm##1 (Figuras 5 e 7) e diz que os resultados de Bob devem ser calculados para satisfazer a conservação do momento angular de spin, enquanto a partição de Bob (Figuras 6 e 7) diz que os resultados de Alice devem ser calculado em média (Respondendo ao desafio de Mermin com conservação sem referencial preferencial).

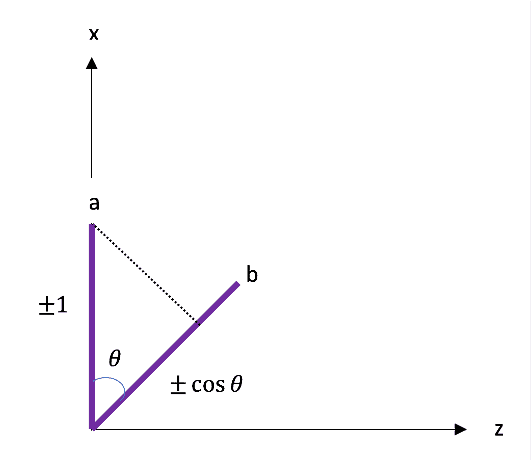
Figura 5

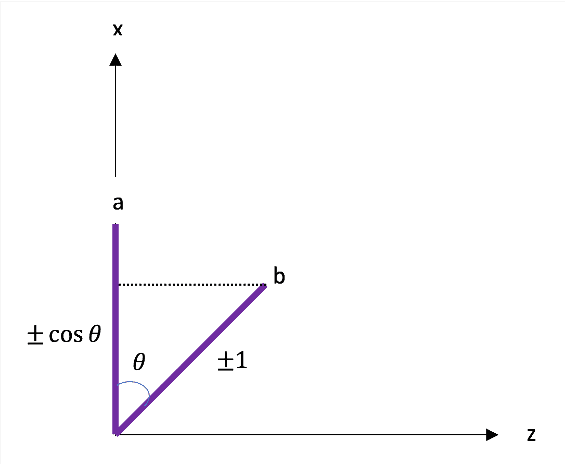
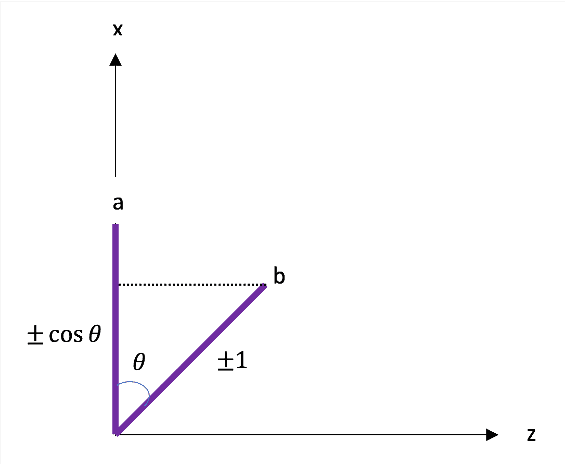
Figura 6

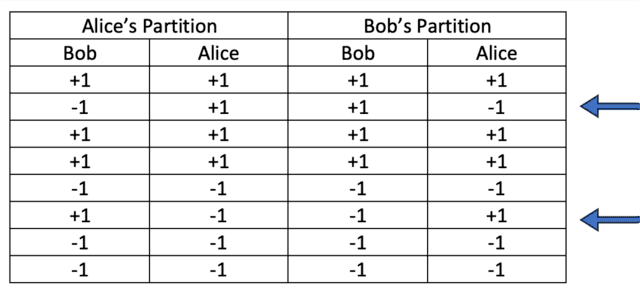
Figura 7

Isto deve lembrá-lo imediatamente de uma situação análoga na RS. Lá, quando Alice e Bob ocupam diferentes referenciais por meio de movimento relativo, eles dividem os eventos do espaço-tempo por suas superfícies de simultaneidade e mostram claramente que as réguas de medição um do outro são curtas. Considere os seguintes eventos:

• Evento 1: Joe, de 20 anos, e Sara, de 20, se encontram.
• Evento 2: Bob, de 20 anos, e Alice, de 17,5 anos, se encontram.
• Evento 3: Bob, de 22 anos, e Kim, de 20, se encontram.

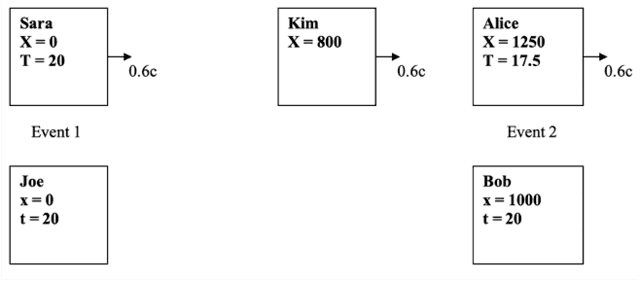
Figura 8

Existem três irmãs (Sara, Kim e Alice) em um referencial movendo-se a 0,6c em relação ao referencial de dois irmãos (Joe e Bob). Os meninos têm a mesma idade no seu referencial e as meninas têm a mesma idade no seu referencial. Isso estabelece simultaneidade para cada conjunto, ou seja, os eventos são simultâneos para os meninos se os eventos ocorrerem quando os meninos tiverem a mesma idade, por exemplo, Eventos 1 e 2 (Figura 8). O mesmo se aplica às meninas, por exemplo, Eventos 1 e 3 (Figura 9). (As diferenças de horário são exageradas para efeito.)

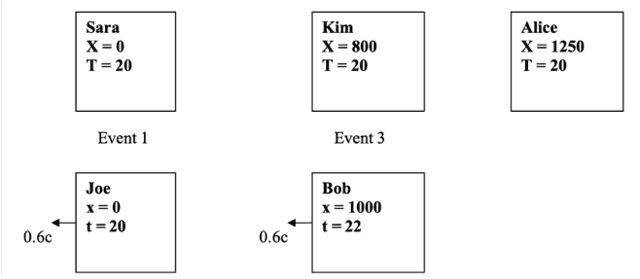
Figura 9

De acordo com a partição de Bob (Figura 8), a distância entre Sara e Alice é de 1.000 km, enquanto Alice diz que é de 1.250 km. Claramente, a partição dos dados de Bob mostra que as réguas de medição de Alice são curtas. Mas, de acordo com a partição de Alice (Figura 9), a distância entre Joe e Bob é de 800 km, enquanto Bob diz que é de 1.000 km. Claramente, a partição dos dados de Alice mostra que as réguas de medição de Bob são curtas.

Em outras palavras, o mistério das correlações que violam a desigualdade de Bell do emaranhamento quântico reside na conservação ‘somente média’ que resulta de “nenhum quadro de referência preferencial” (NPRF), dando a independência do observador de h (NPRF + h). E o mistério da contração do comprimento reside na relatividade da simultaneidade que resulta de “nenhum referencial preferido”, dando ao observador independência de c (NPRF + c).

Então, quais medidores são curtos? Esta questão surge da perspectiva construtiva (errada): não existe um mecanismo causal para encurtar as réguas do medidor na RS. A contração do comprimento não é um efeito dinâmico, é um fato cinemático devido ao postulado da luz, justificado pelo princípio da relatividade.

Da mesma forma, quem deve calcular a média de seus dados para conservar o momento angular de spin? Esta questão surge na perspectiva construtiva (errada): não existe um mecanismo superdeterminístico não native ou retrocausal responsável pelas correlações de QM que violam a desigualdade de Bell. A conservação ‘apenas média’ não é um efeito dinâmico, é um facto cinemático devido ao postulado de Planck, conforme justificado pelo princípio da relatividade.

Os teóricos da informação quântica mostraram que é possível pensar na MQ como uma teoria de princípios, assim como a SR. Esta explicação principal das correlações que violam a desigualdade de Bell não requer mecanismos não locais, superdeterminísticos ou retrocausais, exatamente como a explicação principal da contração do comprimento não requer o éter luminífero. No entanto, a física do programa de reconstrução quântica descreve claramente a realidade.

Referências

1. C. Rovelli, “Mecânica Quântica Relacional”, Worldwide Journal of Theoretical Physics 35, 1637–1678 (1996).
2. A. Zeilinger, “Um Princípio Basic para a Mecânica Quântica”, Foundations of Physics 29(4), 631–643 (1999).
3. G. Chiribella, G. D’Ariano e P. Perinotti, “Teorias probabilísticas com purificação”, Bodily Assessment A 81, 062348 (2010).
4. L. Masanes e M. Mueller, “Uma derivação da teoria quântica a partir de requisitos físicos”, New Journal of Physics 13, 063001 (2011).
5. A. Einstein, “O que é a Teoria da Relatividade?” Londres Instances, 53–54 (1919).
6. C. Brukner e A. Zeilinger, “Invariância de Informação e Probabilidades Quânticas”, Foundations of Physics 39(7), 677–689 (2009).